Example of Functional Data Explorer
Example of Functional Data Explorer
This example analyzes weekly weather data collected from 16 weather stations across the United States. Run the Weather Station Locations script in the data table to view a map of the locations. Daily temperatures are summarized as weekly averages. Not every weather station has a weekly temperature measurement for every week of the year. This is an example of sparse functional data.
1. Select Help > Sample Data Library and open Functional Data/Weekly Weather Data.jmp.
2. Select Analyze > Specialized Modeling > Functional Data Explorer.
3. Select TMAX and click Y, Output.
4. Select Week of Year and click X, Input.
5. Select ID and click ID, Function.
6. Click OK.
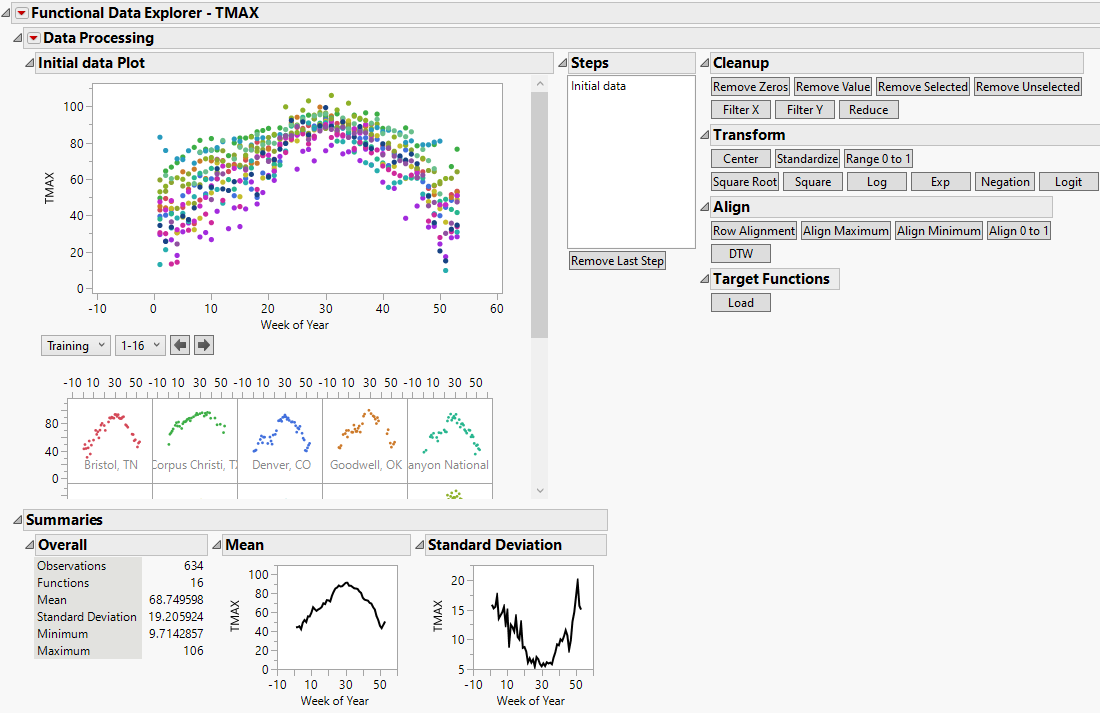
Figure 16.2 Initial Functional Data Explorer Report
The initial Functional Data Explorer report contains plots of the raw data, summary statistics, and summary plots for the functional mean and functional standard deviation of the data. There are also buttons for data processing options. Data processing options are also accessible from the Data Processing red triangle menu. Prior to modeling, it is often a good idea to standardize your output data.
7. Click the Standardize button under the Transform menu.
The data plots and summary statistics are updated based on the specified transformation. Standardized is added to the Steps list.
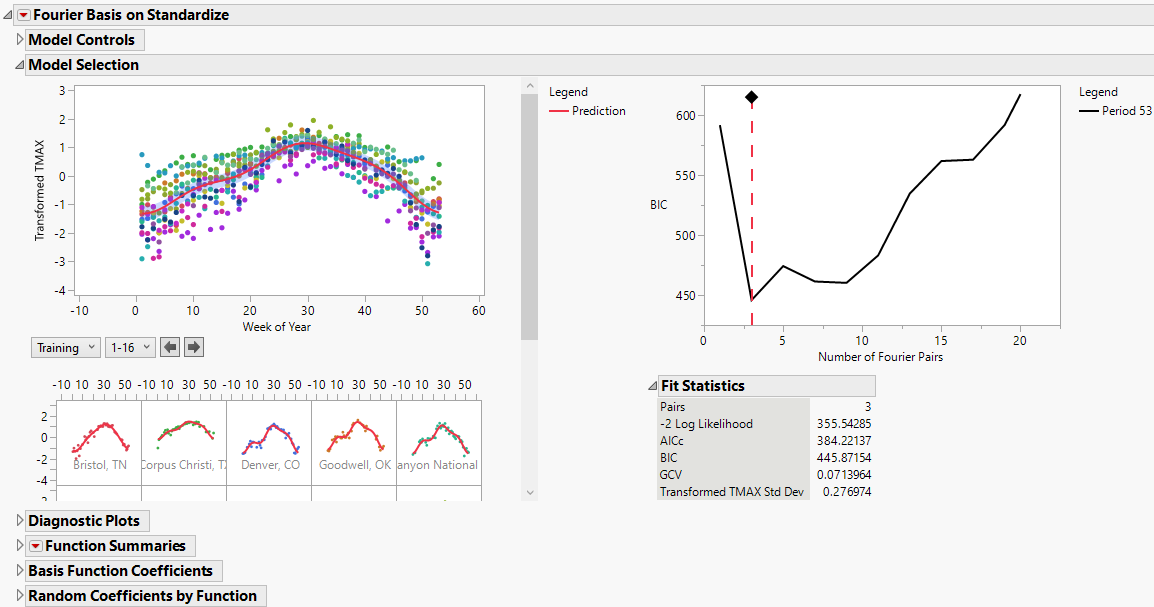
8. Click the Functional Data Explorer red triangle and select Models > Fourier Basis.
Figure 16.3 Fourier Basis Model Report
The Fourier Basis report includes several reports that contain information about the selected model. In the Model Selection report, the displayed model is the best fitting model according to the BIC fit criterion. For the weather data, the Fourier Basis model that is chosen has a period of 53 and three basis function pairs. Fit statistics and coefficients are also available for the model. Scroll down to view the Functional PCA report.
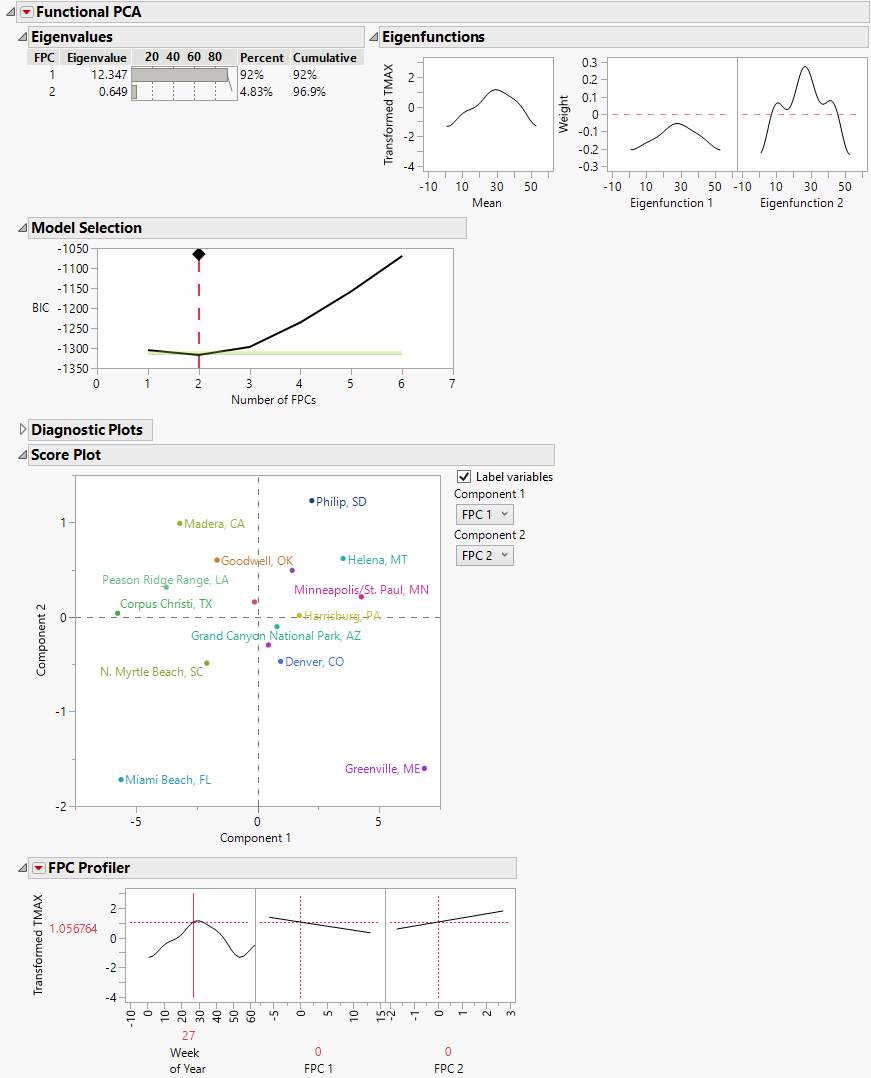
Figure 16.4 Functional PCA Report
The Functional PCA report shows that the first two eigenvalues explain nearly 97% of the variation in the data. In the Model Selection graph, click and drag the red dashed line to 3 FPCs to see that the first three eigenvalues explain 99% of the variation in the data. However, the first eigenvalue alone explains 92%. You can use the Score Plot to detect individual functions that are outliers from the other functions. In the Score Plot, most of the locations are clustered together except for the Miami Beach, FL and Greenville, ME locations. Scroll up to the individual function plots. The function for the Miami Beach location is flatter, indicating less temperature variability than the rest of the locations. The function for the Greenville location has a lower maximum, indicating consistently colder temperatures than the rest of the locations.
Tip: Deselect the Label variables option in the Score Plot report to better identify outliers.