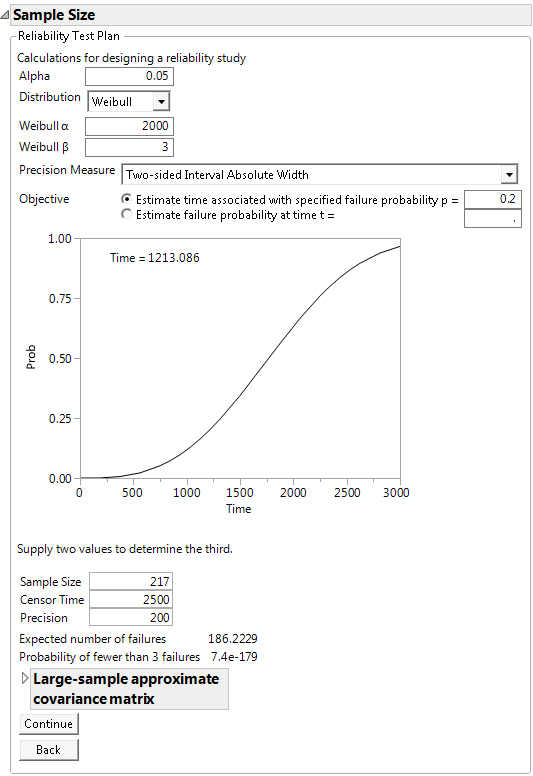
Example of the Reliability Test Plan Calculator
A company has developed a new product and wants to calculate how many units to test to estimate the time until 20% of units fail, using a 95% confidence interval with two-sided absolute precision of 200 hours. In other words, when a confidence interval is created for the estimated time, the difference between the upper and lower limits should be approximately 200 hours. The company can run the test for 2,500 hours. In addition, from studies of similar products, they believe the approximate failure distribution to be a Weibull distribution with location parameter α = 2000 and scale parameter β = 3.
To compute the required sample size:
1. Select DOE > Design Diagnostics > Sample Size and Power.
2. Click Reliability Test Plan.
3. Leave Alpha set at 0.05.
4. Select Weibull from the Distribution list.
5. Enter 2000 for the Weibull α parameter.
6. Enter 3 for the Weibull β parameter.
7. Select Two-sided Interval Absolute Width from the Precision Measure list.
8. Select Estimate time associated with specified failure probability and enter 0.2 for p.
Note: The cumulative distribution function plot is labeled according to the study objective. Here, Time = 1213 is the time estimate for 20% of unit failures.
9. Leave Sample Size blank.
10. Enter 2500 for Censor Time.
11. Enter 200 for Precision.
12. Click Continue.
Figure 17.17 Reliability Test Plan Calculator
To estimate the time until 20% of units fail with a precision of 200 hours requires 217 units on test for 2,500 hours. The expected number of failures in this test is approximately 186, much larger than the minimum of 3 needed to estimate the failure distribution.