Extrapolation Control Metrics
Leverage
In models that are fit in the Standard Least Squares personality of the Fit Model platform, the leverage at the factor settings is used as the extrapolation metric.
The leverage of the ith observation, hii, is the ith diagonal entry of the matrix X(X′X)-1X′, sometimes called the hat matrix. The leverage for a new prediction point is calculated as hpred = x′pred(X′X)-1xpred. The following two criteria can be used to determine if a prediction with leverage hpred is an extrapolation:
• hpred > K × max(hii), where K is a customizable multiplier
• hpred > L × p/n, where L is a customizable multiplier, p is the number of variables, n is the number of observations, and p/n is the average leverage
You can use the Set Threshold Criterion option to specify which criterion is used and the value of the multiplier. The default values of the multipliers are K = 1 and L = 3.
Note: Extrapolation control on profilers run from the graph menu using a saved least squares model do not implement the leverage methodology. Instead, the Regularized Hotelling's T2 methodology is used.
Regularized Hotelling’s T2
In models other than least squares models, the Regularized Hotelling’s T2 value is used as the extrapolation metric. The T2 value for the training data and T2 values for the prediction points are calculated as follows:
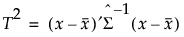
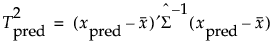
where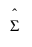 
is the Schafer and Strimmer regularized covariance matrix estimator estimated on the training data. The target matrix used for the Schafer Strimmer estimator is a diagonal covariance matrix. See Schafer and Strimmer (2005). In platforms that train models using observations with missing values, the covariance matrix is estimated with pairwise deletion.
Note: Categorical variables are converted to indicator variables for these calculations.
The calculation of the threshold depends on the number of nonmissing T2 values computed on the training data.
• If there are ten or more nonmissing T2 values, the threshold is set as follows:
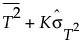
where
K is a customizable multiplier and is set to 3 by default
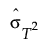is the standard deviation of the T2 values.
• If there are less than ten nonmissing T2 values, the threshold is set using an F distribution quantile equivalent to a Kσ limit.
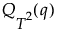
where
q= Φ(K)
Φ(·) is the standard normal distribution
K is a customizable multiplier and is set to 3 by default
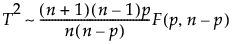
p is the number of parameters
n is the number of nonmissing T2 values