Power Details Window and Reports
The Power Details window and reports are the same as those in the general fitting platform launched by the Fit Model platform. For more information about power calculation, see Power Calculations in Fitting Linear Models.
For each of four columns Alpha, Sigma, Delta, and Number, fill in a single value, two values, or the start, stop, and increment for a sequence of values (Figure 6.32). Power calculations are performed on all possible combinations of the values that you specify.
Alpha (α)
Significance level, between 0 and 1 (usually 0.05, 0.01, or 0.10). Initially, a value of 0.05 shows.
Sigma (σ)
Standard error of the residual error in the model. Initially, RMSE, the estimate from the square root of the mean square error is supplied here.
Delta (δ)
Raw effect size. For more information about effect size computations, see Effect Size in Fitting Linear Models. The first position is initially set to the square root of the sums of squares for the hypothesis divided by n (that is, 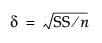 ).
).
Number (n)
Total sample size across all groups. Initially, the actual sample size is put in the first position.
Solve for Power
Solves for the power (the probability of a significant result) as a function of all four values: α, σ, δ, and n.
Solve for Least Significant Number
Solves for the number of observations needed to achieve approximately 50% power given α, σ, and δ.
Solve for Least Significant Value
Solves for the value of the parameter or linear test that produces a p-value of α. This is a function of α, σ, n, and the standard error of the estimate. This feature is available only when the X factor has two levels and is usually used for individual parameters.
Adjusted Power and Confidence Interval
When you look at power retrospectively, you use estimates of the standard error and the test parameters.
– Adjusted power is the power calculated from a more unbiased estimate of the non-centrality parameter.
– The confidence interval for the adjusted power is based on the confidence interval for the non-centrality estimate.
Adjusted power and confidence limits are computed only for the original Delta, because that is where the random variation is.