Robust PCA Outliers
You can use the Robust PCA Outliers utility to quickly identify outlier cells in correlated multivariate data. This method is useful because many other multivariate approaches identify only the outlier rows. Before the method is applied to the data, the columns are first centered (optional) and scaled. The scaling factor is defined as follows:
max [Q(.75) - Q(.50), Q(.50) - Q(.25)] / [normalQuantile(0.75)]
where
Q(p) is the pth quantile
Note: If Q(75) or Q(25) are equal to the median, then more extreme quantiles are used until there is a non-zero range.
After the data are centered and scaled, the Robust PCA Outliers utility performs a sequence of singular value decompositions and thresholding steps to decompose the data matrix. The data are decomposed into a low-rank matrix and a sparse matrix of residuals. The thresholding is done so that the residuals are either very large or outliers or very close to zero for non-outliers. The algorithm determines a matrix rank appropriate to capture the systematic variation without the outliers or small noise. Outliers that are not in the low-rank space are detected based on their residuals. See Candes et al (2009) and Lin et al (2013). If there are missing values, they are initially replaced with zeros after the centering and scaling steps. Then, after each singular value decomposition (SVD) iteration, the missing values are updated by their predicted values from the SVD.
Robust PCA Outliers Report
When you select Robust PCA Outliers from the list of commands, you must specify a value for Lambda and select if the data should be centered. If you Shift+Click the Robust PCA Outliers button, the following options are also available:
Lambda
Specifies a value that determines the sparsity of the matrix of residuals. For larger values of Lambda, the matrix of residuals is more sparse. For a data table with n training rows and p columns, the default value of Lambda is defined as follows:
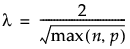
Max Iterations
Specifies the maximum number of SVD iterations.
Converge Criterion
Determines when to stop the algorithm.
Outlier Threshold
Specifies the outlier threshold that determines which outliers are shown in the Cell Large Residuals table. An observation is shown if the scaled residuals is larger than the following:
min[0.99 × max{abs(residuals)}, Outlier Threshold]
By default, the Outlier Threshold is 2.
Center
Determines if the data are centered before the Robust PCA Outlier algorithm is performed.
Note: If the number of rows is less than or equal to 10, the data are not centered.
Scale
Determines if the data are scaled before the Robust PCA Outlier algorithm is performed.
Note: If the number of rows is less than or equal to 10, the data are not scaled.
The Robust PCA Outliers report contains a table with information about the method. This table includes the rank of the low-rank matrix, the number of SVD iterations, the convergence criterion, the value of Lambda, and the number of imputed missing values. The report also contains the following tables and reports:
Cell Large Residuals
A table that shows the largest outlier cells. The number of cells shown is determined by the Outlier Threshold. The table contains the column name and row number of the cell, the residual value, and the scaled residual value.
Tip: To color specific outlier cells in the data table, select rows in the Cell Large Residuals table and click Colorize.
Row Root Mean Square
A table that shows the root mean square value for each row in the data table. The root mean square is calculated using the scaled residuals.
Tip: If you select a row in the Row Root Mean Square table, the corresponding row is selected in the data table.
Column Root Mean Square
A table that shows the root mean square value for each column specified in the launch window. The root mean square is calculated using the scaled residuals.
Tip: If you select a row in the Column Root Mean Square table and click Select Columns, the corresponding column is selected in the data table.
Snapshot
A graphical representation of the outlier cells in the data table. The outlier cells are colored in red.
Residuals
The matrix of residuals from the matrix decomposition. A cell is colored if the absolute value of the scaled residual is greater than the following:
min[0.99 × max{abs(residuals)}, Outlier Threshold]
Low Rank Approximation
The matrix of scaled residuals from the matrix decomposition.
Singular Values
The vector of singular values from the SVD.
Robust PCA Outliers Options
There are buttons at the bottom of the Robust PCA Outliers report that provide options to save different parts of the report.
Close
Closes the Robust PCA Outliers report.
Save Large Outliers
Saves the information in the Cell Large Residuals table to a new data table.
Save Cleaned
Opens a window that provides several techniques to clean the outliers based on thresholds and save new columns to the data table.
Trim
Trims outlier cells if the corresponding absolute scaled residual is greater than the specified threshold. By default, the threshold is 10. Select Color  to color the outlier cells red. The trimmed cells are set to the value of the unscaled threshold.
to color the outlier cells red. The trimmed cells are set to the value of the unscaled threshold.
Impute
Sets outlier cells to the value of the low rank approximation if the corresponding absolute scaled residual is greater than the specified threshold. By default, the threshold is 100. Select Color  to color these cells green.
to color these cells green.
Make Missing
Sets outlier cells to missing if the corresponding absolute scaled residual is greater than the specified threshold. By default, the threshold is 1000. Select Color  to color these cells blue.
to color these cells blue.
Color imputed from missing 
If selected, colors cells that originally had missing values and were imputed.
Save Residuals
Saves the residuals to new columns in the original data table.
Save Scaled Residuals
Saves the scaled residuals to new columns in the original data table.
Save Low Rank Approx
Saves the low-rank approximation to new columns in the original data table.