Stability Analysis

Stability analysis is used in setting pharmaceutical product expiration dates. Three linear degradation models are fit, and an expiration date is estimated following International Conference on Harmonisation (ICH) guidelines. The ICH guidelines are used for the general framework of determining if batches can be pooled for expiration dating (ICH Q1E 2003). For specific implementation details, see the STAB macro and FDA guidelines in Chow (2007, Appendix B).

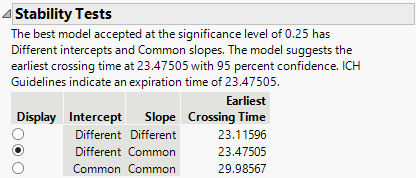
The Stability Tests report summarizes three degradation models and their corresponding earliest crossing times. The best model is selected and displayed in the Overlay plot. The models are listed in the order of complexity.

The first model fits different intercepts and different slopes to each batch. (In the procedure steps and model comparisons described below, this is the full model.) When this model is used for estimating the expiration date, the mean square error (MSE) is not pooled across batches. Prediction intervals are computed for each batch using individual mean squared errors, and the interval that crosses the specification limit first is used to estimate the expiration date. The earliest crossing times are based on 95% two-sided prediction intervals when there are two specification limits provided; the earliest crossing times are based on 95% one-sided prediction intervals when there is only one specification limit provided.

The second model fits different intercepts to each batch, but fits a common slope across all batches. The third model fits a common intercept and a common slope across all batches. When this model is appropriate, it provides the expiration date furthest into the future.

Figure 7.24 Stability Tests Summary 

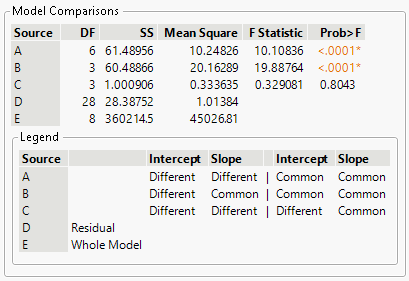
The Model Comparisons section of the Stability Tests report summarizes the tests of significance for each of the stability models. The Legend describes each source. The procedure for determining the best model for expiration dating considers the p-values for Sources C and B. The sources are listed below in reverse order to accommodate the order of steps in the procedure.

Tip: The ICH guidelines specify using a significance level of 0.25 to determine the appropriate model. You can follow the steps below and compare the p-values at each source to a different significance level. If this results in a different model being selected, you can use the radio buttons in the Display column of the table in the Stability Tests summary report.

Source E

Specifies the sum of squared responses minus the Source D sum of squares. The value in the Mean Square column for Source E is the Source E SS value divided by the Source E degrees of freedom, which are equal to the number of parameters in the full model (different intercepts and different slopes).

Source D

Specifies the error sum of squares and corresponding MSE for the full model (different intercepts and different slopes).

Source C

Specifies the test of equal slopes. This is a test of the second model (different intercepts and common slope) versus the full model (different intercepts and different slopes).

– If the p-value is less than 0.25, the slopes are assumed to be different across batches. The procedure stops and the full model (different intercepts and different slopes) is used to estimate the expiration date.

– If the p-value is greater than or equal to 0.25, the slopes are assumed to be common across batches and you then evaluate the intercepts using Source B.

Source B

Specifies the test for equal intercepts. This is a test of the third model (common intercepts and common slopes) versus the second model (different intercepts and common slope).

– If the p-value is less than 0.25, the intercepts are assumed to be different across batches, and the second model (different intercepts and common slope) is used to estimate the expiration date.

– If the p-value is greater than or equal to 0.25, the intercepts are assumed to be common across batches, and the third model (common intercepts and common slopes) is used to estimate the expiration date.

Source A

Specifies the test of the third model (common intercepts and common slopes) versus the full model (different intercepts and different slopes). This test is not used in the procedure to determine the best model for expiration dating.

Figure 7.25 Stability Model Comparisons 

The Reports section contains models fit by the Test Stability option. The following four models are fit by the Test Stability option:

• A different intercept, different slope model where the MSE (mean squared error) is pooled across batches. (This is an alternative to the first model in the Summary report.)

• A different intercept, common slope model. (This is the second model in Summary report.)

• A common intercept, common slope model. (This is the third model in Summary report.)

• A different intercept, different slope model where the MSE (mean squared error) is not pooled across batches. (This is the first model in the Summary report.)

Caution: In addition to the four models fit by the Test Stability option, the Reports section also contains any models fit in the Degradation platform prior to running the Test Stability option.

Example

Use the data in the Stability.jmp sample data table to establish an expiration data for a new product. The data consists of product concentration measurements on four batches. A concentration of 95 is considered the end of the product’s usefulness.

To perform the stability analysis, do the following steps:

1. Select Help > Sample Data Library and open Reliability/Stability.jmp.

2. Select Analyze > Reliability and Survival > Degradation.

3. Select the Stability Test tab.

4. Select Concentration (mg/Kg) and click Y, Response.

5. Select Time and click Time.

6. Select Batch Number and click Label, System ID.

7. Enter 95 for the Lower Spec Limit.

8. Click OK.

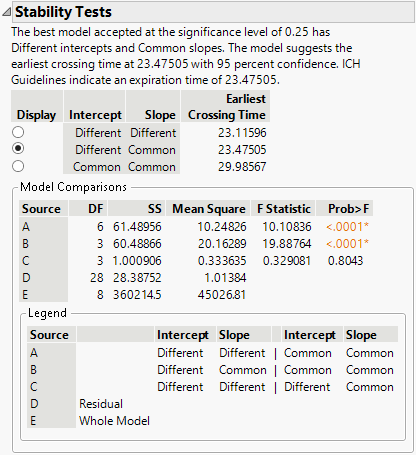
Figure 7.26 Stability Models 

The test for equal slopes has a p-value of 0.8043. Because this is larger than a significance level of 0.25, the test is not rejected, and you conclude the degradation slopes are equal between batches.

The test for equal intercepts and slopes has a p-value of <.0001. Because this is smaller than a significance level of 0.25, the test is rejected, and you conclude that the intercepts are different between batches.

Because the test for equal slopes was not rejected, and the test for equal intercepts was rejected, the chosen model is the one with Different Intercepts and Common Slope. This model is the one selected in the report, and gives an estimated expiration date of 23.475.