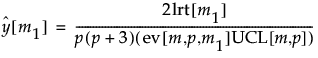Statistical Details for Change Point Detection
This discussion follows the development in Sullivan and Woodall (2000).
Assumptions
Denote a multivariate distribution of dimension p with mean vector μi and covariance matrix Σi by Np(μi,Σi). Suppose that the xi are m (where m > p) independent observations from such a distribution:
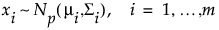
If the process is stable, the means μi and the covariance matrices Σi equal a common value so that the xi have a Np(μ, Σ) distribution.
Suppose that a single change occurs in either the mean vector or the covariance matrix, or both, between the m1 and m1+1 observations. Then the following conditions hold:
• Observations 1 through m1 have the same mean vector and the same covariance matrix (μa,Σa).
• Observations m1 + 1 to m have the same mean vector and covariance matrix (μb,Σb).
• One of the following occurs:
– If the change affects the mean, μa ≠ μb .
– If the change affects the covariance matrix, Σa ≠ Σb.
– If the change affects both the mean and the covariance matrix, μa ≠ μb and Σa ≠ Σb.
Overview
A likelihood ratio test approach is used to identify changes in one or both of the mean vector and covariance matrix. The likelihood ratio test statistic is used to compute a control chart statistic that has an approximate upper control limit of 1. The control chart statistic is plotted for all possible m1 values. If any observation’s control chart statistic exceeds the upper control limit of 1, this is an indication that a shift occurred. Assuming that exactly one shift occurs, that shift is considered to begin immediately after the observation with the maximum control chart statistic value.
Likelihood Ratio Test Statistic
The maximum value of twice the log-likelihood function for the first m1 observations is defined as follows:
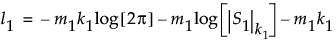
The equation for l1 uses the following notation:
• S1 is the maximum likelihood estimate of the covariance matrix for the first m1 observations.
• k1 = Min[p,m1-1] is the rank of the p x p matrix S1.
• The notation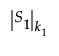 
denotes the generalized determinant of the matrix S1, which is defined as the product of its k1 positive eigenvalues λj:
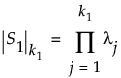
The generalized determinant is equal to the ordinary determinant when S1 has full rank.
Denote the maximum of twice the log-likelihood function for the subsequent m2 = m - m1 observations by l2, and the maximum of twice the log-likelihood function for all m observations by l0. Both l2 and l0 are given by expressions similar to that given for l1.
The likelihood ratio test statistic compares the sum l1 + l2 to l0. The sum l1 + l2 is twice the log-likelihood that assumes a possible shift at m1. The value l0 is twice the log-likelihood that assumes no shift. If l0 is substantially smaller than l1 + l2, the process is assumed to be unstable.
The likelihood ratio test statistic for a test of whether a change begins at observation m1 + 1 is defined as follows:
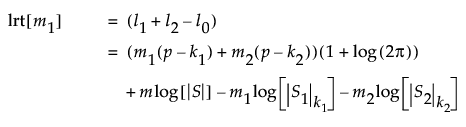
The distribution of the likelihood ratio test statistic is asymptotically chi-square distributed with p(p + 3)/2 degrees of freedom. Large log-likelihood ratio values indicate that the process is unstable.
The Control Chart Statistic
Simulations indicate that the expected value of lrt[m1] varies based on the observation’s location in the series, and, in particular, depends on p and m. See Sullivan and Woodall (2000).
Approximating formulas for the expected value of lrt[m1] are derived by simulation. To reduce the dependence of the expected value on p, lrt[m1] is divided by its asymptotic expected value, p(p + 3)/2.
The formulas for the approximated expected value of lrt[m1] divided by p(p+3)/2 are defined as follows:
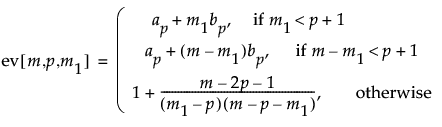
where
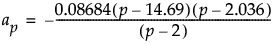
and
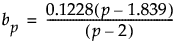
For p = 2, the value of ev[m,p,m1] when m1 or m2 = 2 is 1.3505.
Note: The formulas above are not accurate for p > 12 or m < (2p + 4). In such cases, simulation should be used to obtain approximate expected values.
An approximate upper control limit that yields a false out-of-control signal with probability approximately 0.05, assuming that the process is stable, is calculated as follows:
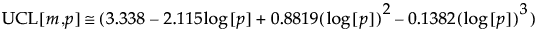
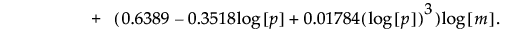
Note that this formula depends on m and p.
The control chart statistic is defined to be twice the log of the likelihood ratio test statistic divided by p(p + 3), divided by its approximate expected value, and also divided by the approximate value of the control limit. Because of the division by the approximate value of the UCL, the control chart statistic can be plotted against an upper control limit of 1. The approximate control chart statistic is calculated as follows:
