Statistical Details for the Agreement Report
The simple Kappa coefficient is a measure of inter-rater agreement.
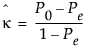
where:
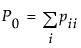
and:
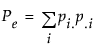
If you view the two response variables as two independent ratings of the n parts, the Kappa coefficient equals +1 when there is complete agreement of the raters. When the observed agreement exceeds chance agreement, the Kappa coefficient is positive, and its magnitude reflects the strength of agreement. Although unusual in practice, Kappa is negative when the observed agreement is less than the chance agreement. The minimum value of Kappa is between -1 and 0, depending on the marginal proportions.
Estimate the asymptotic variance of the simple Kappa coefficient with the following equation:
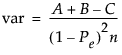
where:
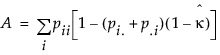
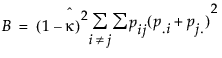
and:
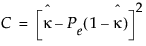
The Kappas are plotted and the standard errors are also given.
Note: The Kappa statistics in the Attribute Chart platform are shown even when the levels of the variables are unbalanced.
Categorical Kappa statistics (Fleiss 1981) are found in the Agreement Across Categories report.
Given the following assumptions:
• n = number of parts (grouping variables)
• m = number of raters
• k = number of levels
• ri = number of reps for part i (i = 1,...,n)
• Ni = m x ri. Number of ratings on part i (i = 1, 2,...,n). This includes responses for all raters, and repeat ratings on a part. For example, if part i is measured 3 times by each of 2 raters, then Ni is 3 x 2 = 6.
• xij = number of ratings on part i (i = 1, 2,...,n) into level j (j=1, 2,...,k)
The individual category Kappa is defined as follows:
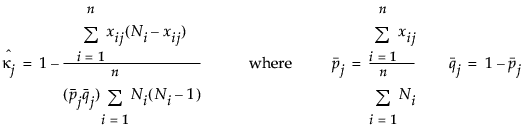
The overall Kappa is defined as follows:
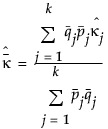
The variance of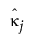 
and 
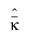are calculated as follows:
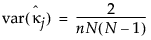
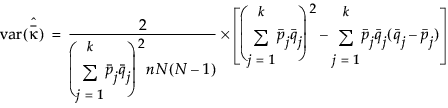
The standard errors of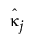 
and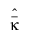 
are shown only when there are an equal number of ratings per part (for example, Ni = N for all i =1,…,n).