Statistical Details for the Misclassification Probabilities
This section describes the computations for the probabilities in the Misclassification Probabilities report. The misclassification probabilities are based on the joint probability function of Y, the measured value of the part, and X, the true value of the part. The joint probability distribution function FYX(y, x) uses a bivariate normal distribution with mean vector [μ, μ] and the following covariance matrix:
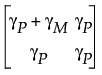
where γP is the part-to-part variation, γM is the measurement variation, and μ is the grand mean. These quantities can be found or derived from quantities in the report window. Specifically, γP + γM is equal to the square of Total Variation (TV) divided by 6: (TV/6)2 and γP is equal to the square of Part Variation (PV) divided by 6: (PV/6)2. The correlation ρYX between Y and X is defined as the square root of γP/(γP + γM).
Next, define the following probabilities:
δ = P[(LSL ≤ X ≤ USL) and (Y < LSL or Y > USL)]
β = P[(X < LSL or X > USL) and (LSL ≤ Y ≤ USL)]
π = P(LSL ≤ X ≤ USL)
These probabilities can be expressed in terms of the joint probability distribution function FYX(y, x) and the marginal probability distribution functions for Y and X: FY(y) and FX(x):
δ = FYX(LSL, USL) - FYX(LSL, LSL) - FYX(USL, USL) + FYX(USL, LSL) + FX(USL) - FX(LSL)
β = FYX(USL, LSL) - FYX(LSL, LSL) - FYX(USL, USL) + FYX(LSL, USL) + FY(USL) - FY(LSL)
π = FX(USL) - FX(LSL)
P(Good part is falsely rejected) = δ/π
P(Bad part is falsely accepted) = β/(1-π)
P(Part is good and is rejected) = δ
P(Part is bad and is accepted) = β
P(Part is good) = π