Formulas for Metrics
The formulas for Coverage and Diversity depend on whether there are constraints. The following notation is used:
uCv is the number of combinations of u things taken v at a time
t is the strength of the design
K is the number of factors
M = KCt
i = 1, 2,..., M is an index that orders all combinations, or projections, of t factors
vik is the number of levels for the kth factor
ni is the number of distinct t tuples in the design for the ith projection
pi is the product of the vik for the factors in the ith projection
r is the number of runs in the design
Unconstrained Design
Coverage and Diversity are given by the following:
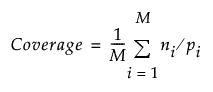
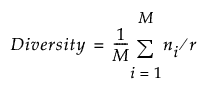
Constrained Design
In a constrained design, certain t tuples are not allowed. This can result in missing values for some t tuples. For some combinations of t factors, there might be no valid t tuples whatsoever. Coverage and diversity must be defined in terms of the possible valid combinations. For this reason, the formulas for constrained designs require additional notation:
ai is the number of invalid t tuples arising from factors in the ith projection
m is the number of projections where there are no valid t tuples
qi is the number of runs in the design with missing values for any factor in the ith projection
ri = r - qi
M ′ = M - m
Coverage and Diversity are given by the following:
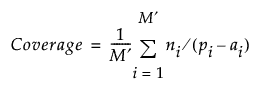
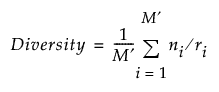
If there are no invalid t tuples (M′ = M) and if there are no missing values (ri = r, for all i), then the definitions for coverage and diversity for constrained designs reduce to the definitions for unconstrained designs. See Morgan (2014).