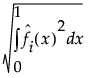Function Summaries Details
The Function Summaries report includes the following summary statistics: integrated difference, root integrated square error (RISE), and root integrated function squared (RIFS). These summary statistics are defined in this section. For all equations in this section, it is assumed that the input values have been aligned between 0 and 1. The following notation is used for all functions:
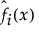 is the estimated function for curve i at input value x
is the estimated function for curve i at input value x
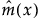 is the estimated mean function at input value x
is the estimated mean function at input value x
Integrated Difference
The integrated difference is the average difference between points on the ID specific curve and the overall mean curve. It can be used to determine if the ID specific curve falls above or below the mean curve, on average. The integrated difference for curve i is defined as follows:
IDi = 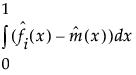
RISE
Root integrated square error (RISE) is the average distance between the ID specific curve and the overall mean curve. It can be used to determine which ID specific curves are most similar or most different from the overall mean curve. The RISE summary value for curve i is defined as follows:
RISEi = 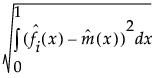
RIFS
Root integrated function squared (RIFS) is a summary value for analyzing optimal curve scenarios. If you pre-subtract off an optimal curve, you can use the smallest values of RIFS to determine which functions are closest to the optimal curve. The RIFS summary value for curve i is defined as follows:
RIFSi =