Margin of Error for One Sample Proportion
Use the Interval Explorer for One Sample Proportion to determine a sample size for a confidence interval. Select DOE > Sample Size Explorers > Confidence Intervals > Margin of Error for One Sample Proportion. Explore the trade offs between the assumed proportion, sample size, significance, and the margin of error for your interval. Calculations use the Normal approximation.
Interval Explorer for One Sample Proportion Options
Set study assumptions and explore sample sizes using the radio buttons, text boxes, and sliders. The curve updates as you make changes to the settings. Alternatively, change settings by dragging the cross hairs on the curve or adjusting the values in the axis text boxes.
Interval Type
Bound
Specifies a one-side of the interval (upper or lower bound)
Interval
Specifies a two-sided interval.
Fixed Parameters
Alpha
Specifies the confidence level, 1 - Alpha. The default alpha level is 0.05 for a 95% confidence interval.
Interval Parameters
Parameters that are inter-related and update as you make changes.
Proportion
Specifies the assumed proportion for the interval.
Sample Size
Specifies the total number of observations (runs, experimental units, or samples) needed to construct your interval.
Margin of Error
Specifies the half-width of the interval. With all other parameters fixed, margin of error decreases as sample size increases.
Save Settings
Saves the current settings to the Saved Settings table. This enables you to save a set of alternative study plans. See Saved Settings in the Sample Size Explorers.
Make Data Collection Table
Creates a new data table that you can use for data collection.
Statistical Details for the One Sample Proportion Interval Explorer
The interval calculations for capturing a population proportion is based on the Agresti-Coull method, see Agresti and Coull(1998).
The margin of error (MOE) for confidence intervals is calculated as follows:
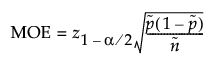
The bound is calculated as follows:
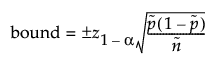
where
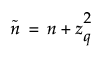
and
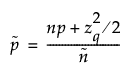
and q = 1 - α/2 for an interval or q = 1 - α for a bound.