Models with Continuous Predictors
If the Gaussian Process model contains only continuous predictors, the Gaussian Process platform implements two possible correlation structures, the Gaussian and the Cubic.
The Gaussian correlation structure uses the product exponential correlation function with a power of 2 as the estimated model. This model assumes that Y is normally distributed with mean μ and covariance matrix σ2R. The elements of the R matrix are defined as follows:
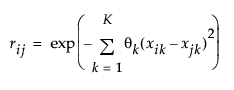
where
K = # of continuous predictors
θk = theta parameter for the kth predictor
xik = the value of the kth predictor for subject i
xjk = the value of the kth predictor for subject j
The Cubic correlation structure also assumes that Y is normally distributed with mean μ and covariance matrix σ2R. The R matrix consists of the following elements:
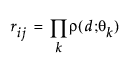
where
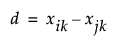
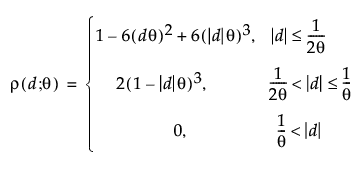
See Santer (2003). The theta parameter used in the Cubic correlation structure is the reciprocal of the parameter often used in the literature. The reciprocal is used so that when theta has no effect on the model, then rho has a value of zero, rather than infinity.