Statistical Details for the Model Driven Multivariate Control Chart Platform
Monitoring Statistics
T2
The 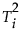 value for each of the i observations is plotted on the T2 control chart. For historical and current data, the T2 values for a PCA or PLS model with k components are defined as:
value for each of the i observations is plotted on the T2 control chart. For historical and current data, the T2 values for a PCA or PLS model with k components are defined as:
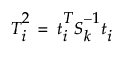
where:
ti = the vector of k scores for the ith observation
Sk = the diagonal sample covariance matrix of the k scores for historical observations
For PCA models, Sk is the diagonal eigenvalue matrix.
The mean of each of the k historical score vectors is 0 when the data is centered during the data preprocessing step. This step occurs in PCA on correlations or covariances and in PLS with centering. For preprocessing options where X is not centered, the data is assumed to have been centered by the user, so the mean of each of the k score vectors is 0. For more information about Hotelling’s T2, see Montgomery (2013).
SPE
For both PCA and PLS models, the preprocessed X matrix can be decomposed as:
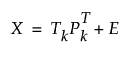
where Tk = (t1,...,tk) is the k dimensional score matrix and Pk = (p1,...,pk) is a matrix with the first k eigenvectors for PCA models or the loading matrix for PLS models. The squared prediction error of this PCA or PLS model is used for the SPE control chart.
The SPEi value for each of the i observations is plotted on the SPE control chart. The squared prediction error is defined as:
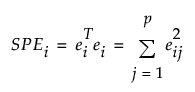
where
ei = the residual vector for observation i
p = number of variables
DModX
The DModXi value for each of the i observations is plotted on the DModX control chart. The normalized distance to model (DModX) is defined as:
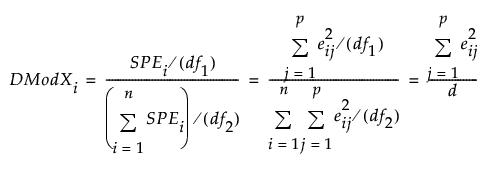
where
eij = the residual for observation i and variable j
df1 = p−k
df2 = (n−k−1)(p−k) if the data is centered and (n−k)(p−k) if the data is not centered
n = number of historical data observations
k = number of PCA/PLS components
p = number of variables
Note: DModXi is equal to SPEi scaled by 1/d.