Multivariate Tests
In the following, E is the residual cross product matrix and H is the model cross product matrix. Diagonal elements of E are the residual sums of squares for each variable. Diagonal elements of H are the sums of squares for the model for each variable. In the discriminant analysis literature, E is often called W, where W stands for within.
Test statistics in the multivariate results tables are functions of the eigenvalues λ of 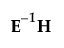 . The following list describes the computation of each test statistic.
. The following list describes the computation of each test statistic.
Note: After specification of a response design, the initial E and H matrices are premultiplied by M′ and postmultiplied by M.
• Wilks’ Lambda
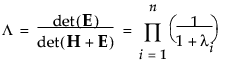
• Pillai’s Trace
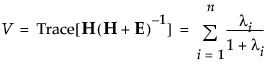
• Hotelling-Lawley Trace
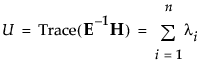
• Roy’s Max Root
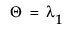 , the maximum eigenvalue of
, the maximum eigenvalue of 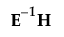 .
.
E and H are defined as follows:
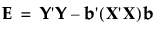
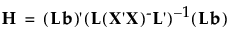
where b is the estimated vector for the model coefficients and A- denotes the generalized inverse of a matrix A.
The whole model L is a column of zeros (for the intercept) concatenated with an identity matrix having the number of rows and columns equal to the number of parameters in the model. L matrices for effects are subsets of rows from the whole model L matrix.