Overview of the Fit Proportional Hazards Platforms
The proportional hazards model is a special semiparametric regression model proposed by D. R. Cox (1972) to examine the effect of explanatory variables on survival times. The survival time of each member of a population is assumed to follow its own hazard function.
The proportional hazards model is nonparametric in the sense that it involves an unspecified arbitrary baseline hazard function. It is parametric because it assumes a parametric form for the covariates. The baseline hazard function is scaled by a function of the model’s (time-independent) covariates to give a general hazard function. Unlike the Kaplan-Meier analysis, proportional hazards computes parameter estimates and standard errors for each covariate. The regression parameters (β) associated with the explanatory variables and their standard errors are estimated using the maximum likelihood method. A conditional risk ratio (or hazard ratio) is also computed from the parameter estimates.
The survival estimates in proportional hazards are generated using an empirical method. See Lawless (1982). They represent the empirical cumulative hazard function estimates, H(t), of the survivor function, S(t), and can be written as S0 = exp(-H(t)). The hazard function is defined as follows:
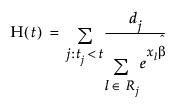
When there are ties in the response, meaning there is more than one failure at a given time event, the Breslow likelihood is used.