Parameterizations for Distributions
This section gives the density functions f for the distributions used in the Process Capability platform. It also gives expected values and variances for all but the Johnson and SHASH distributions.
Normal
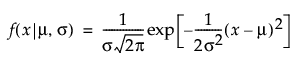 ,
, 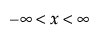 ,
, 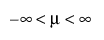 ,
, 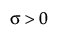
E(X) = μ
Var(X) = σ2
Beta
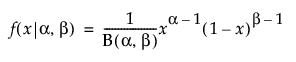 ,
, 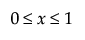 ,
, 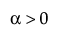 ,
, 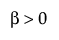
E(X) = 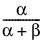
Var(X) = 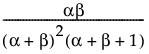
where B(·) is the Beta function.
Exponential
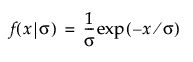 ,
, 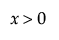 ,
, 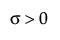
E(X) = σ
Var(X) = σ2
Gamma
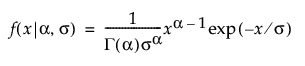 ,
, 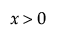 ,
, 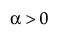 ,
, 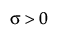
E(X) = ασ
Var(X) = ασ2
where Γ(·) is the gamma function.
Johnson
Johnson Su
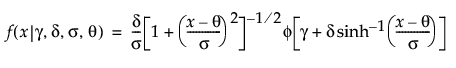 ,
, 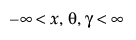 ,
, 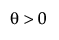 ,
, 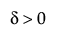
Johnson Sb
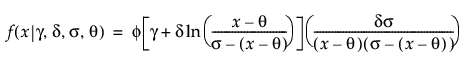 ,
, 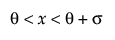 ,
, 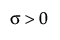
Johnson Sl
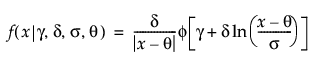 ,
, 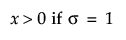 ,
, 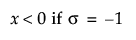
where φ(·) is the standard normal probability density function.
Lognormal
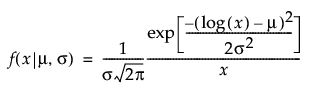 ,
, 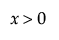 ,
, 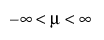 ,
, 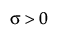
E(X) =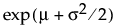
Var(X) =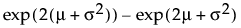
Mixture of Normals
The Mixture of 2 Normals and Mixture of 3 Normals options for Distribution share the following parameterization:
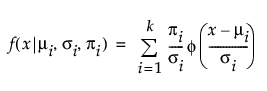
E(X) =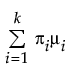
Var(X) =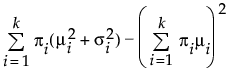
where μi, σi, and πi are the respective mean, standard deviation, and proportion for the ith group, and φ(·) is the standard normal probability density function. For the Mixture of 2 Normals, k is equal to 2. For the Mixture of 3 Normals distribution, k is equal to 3. A separate mean, standard deviation, and proportion of the whole is estimated for each group in the mixture.
SHASH
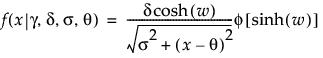 ,
, 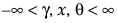 , 0 < δ, 0 < σ
, 0 < δ, 0 < σ
where
φ(·) is the standard normal pdf
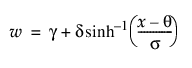
Note: When γ = 0 and δ = 1, the SHASH distribution is equivalent to the normal distribution with location θ and scale σ.
Weibull
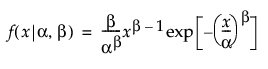 ,
, 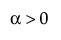 ,
, 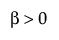
E(X) =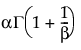
Var(X) =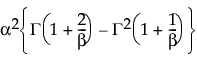
where Γ(·) is the gamma function.