Statistical Details for Discrete Fit Distributions (Legacy)
This section contains statistical details for the options in the Discrete Fit menu.
Note: Some features of distribution fitting have been updated in JMP 15. This section contains details of the older features from previous JMP releases that have been retained for compatibility purposes. These features are available by selecting Continuous Fit > Enable Legacy Fitters in the red triangle menu for a variable.
Poisson
For more information about the Poisson distribution fit, see Fit Poisson.
Gamma Poisson
This distribution is useful when the data are a combination of several Poisson(μ) distributions and each Poisson(μ) distribution has a different μ. One example is the overall number of accidents combined from multiple intersections, when the mean number of accidents (μ) varies between the intersections.
The Gamma Poisson distribution results from assuming that x|μ follows a Poisson distribution and μ follows a Gamma(α,τ). The Gamma Poisson has parameters λ = ατ and σ = τ+1. The parameter σ is a dispersion parameter. If σ > 1, there is over dispersion, meaning there is more variation in x than explained by the Poisson alone. If σ = 1, x reduces to Poisson(λ).
pmf: 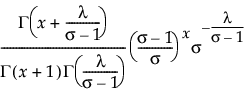 for 0 < λ; 1 ≤ σ; x = 0,1,2,...
for 0 < λ; 1 ≤ σ; x = 0,1,2,...
E(x) = λ
Var(x) = λσ
where Γ(·) is the Gamma function.
Remember that x|μ ~ Poisson(μ), while μ~ Gamma(α,τ). The platform estimates λ = ατ and σ = τ+1. To obtain estimates for α and τ, use the following formulas:


If the estimate of σ is 1, the formulas do not work. In that case, the Gamma Poisson has reduced to the Poisson(λ), and  is the estimate of λ.
is the estimate of λ.
If the estimate for α is an integer, the Gamma Poisson is equivalent to a Negative Binomial with the following pmf:
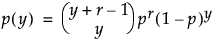 for 0 ≤ y
for 0 ≤ y
with r = α and (1-p)/p = τ.
Run demoGammaPoisson.jsl in the JMP Samples/Scripts folder to compare a Gamma Poisson distribution with parameters λ and σ to a Poisson distribution with parameter λ.
Binomial
For more information about the binomial distribution fit, see Fit Binomial.
Beta Binomial
For more information about the beta binomial distribution fit, see Fit Beta Binomial.