Statistical Details for the Fit Parametric Survival Platform
This section contains statistical details for the Fit Parametric Survival platform.
Loss Formulas for Survival Distributions
The following formulas are for the negative log-likelihoods to fit common parametric models. Each formula uses the calculator if conditional function with the uncensored case of the conditional first and the right-censored case as the Else clause. You can copy these formulas from tables in the Loss Function Templates folder in Sample Data and paste them into your data table.
Exponential Loss Function
In the exponential loss function shown here, sigma represents the mean of the exponential distribution and Time is the age at failure.
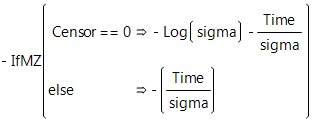
A characteristic of the exponential distribution is that the instantaneous failure rate remains constant over time. This means that the chance of failure for any subject during a given length of time is the same regardless of how long a subject has been in the study.
Weibull Loss Function
The Weibull density function often provides a good model for the lifetime distributions. You can use the Survival platform for an initial investigation of data to determine whether the Weibull loss function is appropriate for your data.
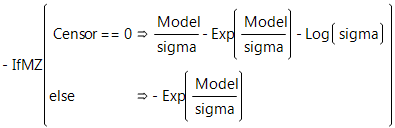
There are examples of one-parameter, two-parameter, and extreme-value functions in the Loss Function Templates folder.
Lognormal Loss Function
The formula shown below is the lognormal loss function where Normal Distribution(model/sigma) is the standard normal distribution function. The hazard function has value 0 at t = 0, increases to a maximum, and then decreases. The hazard function approaches zero as t becomes large.

Loglogistic Loss Function
If Y is distributed as the logistic distribution, Exp(Y) is distributed as the loglogistic distribution.
