Statistical Details for the Multiple Factor Analysis Platform
Multiple factor analysis combines information from sub-tables into a set of orthogonal columns that describe the items in the rows of the table. The basic procedure is as follows:
• Perform PCA on each sub-table.
• Record the first eigenvalue of each sub-table to create a matrix of weights.
• Concatenate the sub-tables side-by-side, center and normalize the matrix.
• Perform a generalized PCA on the concatenated table via the singular value decomposition. Generalized PCA is used to constrain the solution using the sub-table weights.
This results in three matrices of generalized right and left singular vectors and singular values. These are then used to derive component scores, eigenvalues, and component loadings for the consensus across sub-tables. These three matrices are the result of decomposing the many columns from the original measurements into a few interpretable dimensions that explain the similarities and differences between the objects being measured.
Calculations
For MFA, a singular value decomposition of the X matrix can be defined as follows:
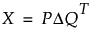 with the constraint
with the constraint 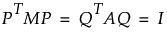
The matrices use are as follows:
X is an n x p centered and normalized matrix of sub-tables. In consumer research there are n products and p panelists’ ratings.
Q is a p x q matrix of right singular vectors, which are weighted by the MFA singular values to obtain the loadings on q principal components.
Δ is a q x q diagonal matrix of singular values from the generalized PCA. As with PCA, the magnitude of the squared singular values, or eigenvalues, represent the importance of each principal component in the combined analysis.
P is an n x q matrix of left singular vectors, which are weighted by the MFA singular values to obtain the q principal components of the compromise.
M is the n x n diagonal matrix of mass weights.
A is the p x p diagonal matrix of block or panelist weights.
For more information about multiple factor analysis, see Abdi et al. (2013).
Mass Weight
JMP calculations use N - 1 for mass weight calculations. These calculations affect individual and block partial scores.