The SVD and the Covariance Matrix
This section describes how the eigenvectors and eigenvalues of a covariance matrix can be obtained using the SVD. When the matrix of interest has at least one large dimension, calculating the SVD is much more efficient than calculating its covariance matrix and its eigenvalue decomposition.
Let n be the number of observations and p the number of variables involved in the multivariate analysis of interest. Denote the n by p matrix of data values by X.
The SVD is usually applied to standardized data. To standardize a value, subtract its mean and divide by its standard deviation. Denote the n by p matrix of standardized data values by Xs. Then the covariance matrix of the standardized data is the correlation matrix for X and is defined as follows:
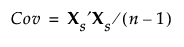
The SVD can be applied to Xs to obtain the eigenvectors and eigenvalues of Xs′Xs. This allows efficient calculation of eigenvectors and eigenvalues when the matrix X is either extremely wide (many columns) or tall (many rows). This technique is the basis for Wide PCA. See Principal Components Report.