The SVD and the Inverse Covariance Matrix
Some multivariate techniques require the calculation of inverse covariance matrices. This section describes how the SVD can be used to calculate the inverse of a covariance matrix.
Denote the standardized data matrix by Xs and define S = Xs′Xs. The singular value decomposition allows you to write S as follows:
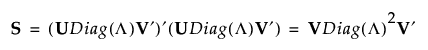
If S is of full rank, then V is a p by p orthonormal matrix, and you can write S-1 as follows:
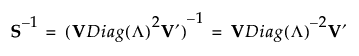
If S is not of full rank, then Diag(Λ)-1 can be replaced with a generalized inverse, Diag(Λ)+, where the diagonal elements of Diag(Λ) are replaced by their reciprocals. This defines a generalize inverse of S as follows:
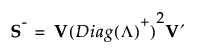
This generalized inverse can be calculated using only the SVD.
For more information about the application of the SVD for wide linear discriminant analysis, see Wide Linear Discriminant Method.