Tolerance Intervals
This section contains statistical details for one-sided and two-sided tolerance intervals.
Normal Distribution-Based Intervals
One-Sided Interval
The one-sided interval is computed as follows:
Lower Limit = 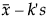
Upper Limit = 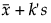
where
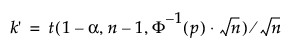
s is the standard deviation
t is the quantile from the non-central t-distribution
Φ-1 is the standard normal quantile
Two-Sided Interval
The two-sided interval is computed as follows:
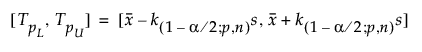
where s is the standard deviation and k(1-α/2; p,n) is a constant.
To determine k, consider the fraction of the population captured by the tolerance interval. Tamhane and Dunlop (2000) define this fraction as follows:
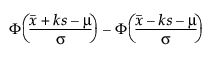
where Φ denotes the standard normal cdf (cumulative distribution function).
Therefore, k solves the following equation:

where 1 - γ is the fraction of all future observations contained in the tolerance interval.
For more information about normal distribution-based tolerance intervals, see Tables J.1a, J.1b, J.6a, and J.6b of Meeker et al. (2017).
Nonparametric Intervals
One-Sided Lower Limit
The lower 100(1 - α)% one-sided tolerance limit to contain at least a proportion β of the sampled distribution from a sample of size n is the order statistic x(l). The index l is computed as follows:
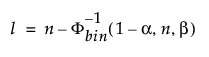
where Φ-1bin(1-α, n, β) is the (1 - α)th quantile of the binomial distribution with n trials and probability of success β.
The actual confidence level is computed as Φbin(n-l, n, β), where Φbin(x, n, β) is the probability of a binomially distributed random variable with n trials and probability of success β being less than or equal to x.
Note that to compute a lower one-sided distribution-free tolerance interval, the sample size n must be at least as large as 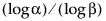 .
.
One-Sided Upper Limit
The upper 100(1 - α)% one-sided tolerance limit to contain at least a proportion β of the sampled distribution from a sample of size n is the order statistic x(u). The index u is computed as follows:
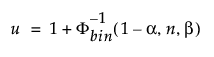
where Φ-1bin(1-α, n, β) is the (1 - α)th quantile of the binomial distribution with n trials and probability of success β.
The actual confidence level is computed as Φbin(u-1, n, β), where Φbin(x, n, β) is the probability of a binomially distributed random variable with n trials and probability of success β being less than or equal to x.
Note that to compute an upper one-sided distribution-free tolerance interval, the sample size n must be at least as large as 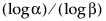 .
.
Two-Sided Interval
The 100(1 - α)% two-sided tolerance interval to contain at least a proportion β of the sampled distribution from a sample of size n is computed as follows:
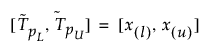
where x(i) is the ith order statistic and l and u are computed as follows:
Let ν = n - Φ-1bin(1-α, n, β), where Φ-1bin(1-α, n, β) is the (1 - α)th quantile of the binomial distribution with n trials and probability of success β. If ν is less than 2, a two-sided distribution-free tolerance interval cannot be computed. If ν is greater than or equal to 2, l = floor(ν/2) and u = floor(n + 1 - ν/2).
The actual confidence level is computed as Φbin(u-l-1, n, β), where Φbin(x, n, β) is the probability of a binomially distributed random variable with n trials and probability of success β being less than or equal to x.
Note that to compute a two-sided distribution-free tolerance interval, the sample size n must be at least as large as the n in the following equation:
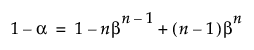
For more information about distribution-free tolerance intervals, see Meeker et al. (2017, sec. 5.3).