Transcendental Functions
Arrhenius(n)
Description
Converts the temperature n to the value of explanatory variable in Arrhenius model.
Returns
11604.5181215503/(n+273.15)
Argument
n
Temperature in Celsius.
Notes
This is frequently used as a transformation.
Arrhenius Inv(n)
Description
The inverse of the Arrhenius function. Converts the value n to the temperature in Celsius.
Returns
(11604.5181215503/n)-273.15
Argument
n
The value of the converted explanatory variable in Arrhenius model.
Notes
This is frequently used as a transformation.
Beta(a, b)
Description
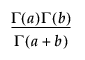
Returns
Returns the beta function.
Arguments
a, b
numbers
Cytometry Logicle(x, T, W, M, A)
Description
Computes a cytometry logicle transformation. For more information about the logicle transformation, see Moore and Parks (2012).
Cytometry Logicle Inverse(y, T, W, M, A)
Description
Computes the inverse cytometry logicle transformation. For more information about the logicle transformation, see Moore and Parks (2012).
Digamma(n)
Description
The derivative of the log of the gamma function (LGamma).
Returns
The digamma function evaluated at n.
Argument
n
A number
Exp(a)
Description
Raises e to the power a.
Returns
ea.
Argument
a
A number
Equivalent Expression
e()^a
ExpM1(x)
Description
Returns a more accurate calculation of Exp(x)-1 when x is very small.
Factorial(n)
Description
Multiplies all numbers 1 through n, inclusive
Returns
The product.
Arguments
n
Any integer
Notes
One and only one argument must be specified.
FFT({list }, <named arguments>)
Description
Conducts a Fast Fourier Transformation (FFT) on a list of matrices.
Returns
The function takes one matrix, or a list of matrices for complex numbers. The returned value is a list of two matrices with the same dimensions as the first argument.
Argument
List
A list of one or two matrices. If one is provided, it is considered to be the real part. If two are provided, the first is the real part and the second is the imaginary part. Both matrices must have the same dimensions, and both must have more than one row.
Optional Named Arguments
<<inverse(Boolean)
If true (1), an inverse FFT is conducted.
<<multivariate(Boolean)
If true (1), a multivariate FFT is conducted. If false(0), a spatial FFT is conducted.
<<scale(number)
Multiplies the return values by the specified number.
Fit Transform To Normal(Distribution("name"), Y(vector), <Freq(vector))
Description
Fits a transformation to normality for a vector of data. This includes the Johnson Sl, Johnson Sb, Johnson Su, and GLog distributions.
Returns
A list that contains parameter estimates, the covariance matrix, the log-likelihood, AICc, a convergence message, and the transformed values. See Likelihood, AICc, and BIC in Fitting Linear Models.
Gamma(t, <limit>)
Description
The gamma function of x, or for each row if x is a column:
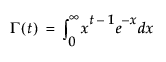
Returns
The gamma.
Arguments
t
a number or a column
limit
optional limit. The default is infinity.
Notes
Gamma(t, limit) is the same integral as Gamma(t) but with the limit of integration that is defined instead of infinity.
LGamma(t)
Description
Returns the log gamma function for t, which is the natural log of gamma.
Ln(n)
Description
Returns the natural logarithm (base e logarithm) of n.
Log(n, <base>)
Description
Returns the natural logarithm (base e logarithm) of n. An optional second argument lets you specify a different base. For example, Log(n,3) for the base 3 logarithm of n. The Log argument can be any numeric expression. The expression Log(e()) evaluates as 1, and Log(32,2) is 5.
Log10(n)
Description
Returns the common (base 10) logarithm of n.
Log1P(n)
Description
Same as Log(1 + x), except that it is more accurate when x is very small.
Logist(x)
Description
Returns 1/(1+Exp(-x)), which converts a number in the domain -∞...+∞ into range 0...1. The function is useful in logistic regression.
Logist Percent(p)
Description
Similar to the Logist() function but with the result scaled from 0 to 100.
Logit(p)
Description
Returns log(p/(1-p)).
Logit Percent(p)
Description
Similar to the Logit() function with the argument 0 to 100 rather than 0 to 1.
N Choose K(n, k)
Description
This function returns the number of n things taken k at a time (“n choose k”) and is computed in the standard way using factorials, as 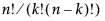 . For example, NChooseK(5,2) evaluates as 10.
. For example, NChooseK(5,2) evaluates as 10.
Notes
This is implemented internally in JMP using lGamma functions. The result is not always an integer.
Power(a, <b>)
a^b
Description
Raises a to the power of b.
Returns
The product of a multiplied by itself b times.
Arguments
a
Can be a variable, number, or matrix.
b
(Optional) Can be a variable or a number.
Notes
For Power(), the second argument (b) is optional, and the default value is 2. Power(a) returns a2.
Root(n, <r>)
Description
Returns the rth root of n, where r defaults to 2 for square root.
SbInv(z, gamma, delta, theta, sigma)
Description
Returns a transformation of a standard normal variable to a double bounded Johnson variable.
SbTrans(x, gamma, delta, theta, sigma)
Description
Returns a transformation of a double bounded Johnson variable to a standard normal variable.
Scheffe Cubic(x1, x2)
Description
Returns x1*x2*(x1-x2). This function supports notation for cubic mixture models.
SHASHInv(z, gamma, delta, theta, sigma)
Description
Returns a transformation of a standard normal variable to a sinh-arcsinh (SHASH) variable. The transformation is calculated as σ*sinh((arcsinh(z)-γ)/δ)+θ.
SHASHTrans(x, gamma, delta, theta, sigma)
Description
Returns a transformation of a sinh-arcsinh (SHASH) variable to a standard normal variable. The transformation is calculated as sinh(γ+δ*arcsinh((x-θ)/σ)).
SlInv(z, gamma, delta, theta, sigma)
Description
Returns a transformation of a standard normal variable to a Johnson Sl variable.
SlTrans(x, gamma, delta, theta, sigma)
Description
Returns a transformation of a Johnson Sl variable to a standard normal variable.
Sqrt(n)
Description
Returns the square root of n.
Squash(expr)
Description
An efficient computation of the function 1/ [1 + exp(expr)].
Squish(expr)
Description
Equivalent to Squash(-expr), or 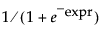 .
.
SuInv(z, gamma, delta, theta, sigma)
Description
Returns a transformation of a standard normal variable to an unbounded Johnson variable.
SuTrans(x, gamma, delta, theta, sigma)
Description
Returns a transformation of an unbounded Johnson variable to a standard normal variable.
Trigamma()
Description
Returns the trigamma function evaluated at n. The trigamma function is the derivative of the digamma function.