Unequal Variances
JMP provides four tests for equality of group variances. When the variances across groups are not equal, the usual assumptions for analysis of variance are not satisfied. For example, the ANOVA F test is not valid and an analysis that does not assume equal group variances should be used. The concept behind the first three tests of equal variances is to perform an analysis of variance on a new response variable constructed to measure the spread in each group. The fourth test is Bartlett’s test, which is similar to the likelihood ratio test under normal distributions. The Unequal Variances option is not available when a Block variable is specified in the launch window.
Note: Another method to test for unequal variances is ANOMV. See Analysis of Means Methods.
The following Tests for Equal Variances are available:
O’Brien
Constructs a dependent variable so that the group means of the new variable equal the group sample variances of the original response. An ANOVA on the O’Brien variable is actually an ANOVA on the group sample variances (O’Brien 1979; Olejnik and Algina 1987).
Brown-Forsythe
Shows the F test from an ANOVA where the response is the absolute value of the difference of each observation and the group median (Brown and Forsythe 1974).
Levene
Shows the F test from an ANOVA where the response is the absolute value of the difference of each observation and the group mean (Levene 1960). The spread is measured as 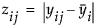 (as opposed to the SAS default
(as opposed to the SAS default 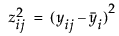 ).
).
Bartlett
Compares the weighted arithmetic average of the sample variances to the weighted geometric average of the sample variances. The geometric average is always less than or equal to the arithmetic average with equality holding only when all sample variances are equal. The more variation there is among the group variances, the more these two averages differ. A function of these two averages is created, which approximates a χ2-distribution (or, in fact, an F distribution under a certain formulation). Large values correspond to large values of the arithmetic or geometric ratio, and therefore to widely varying group variances. Dividing the Bartlett Chi-square test statistic by the degrees of freedom gives the F value shown in the table. Bartlett’s test is not very robust to violations of the normality assumption (Bartlett and Kendall 1946).
F Test 2-sided
(Available only if there are two levels of the X variable.) If there are only two groups tested, then a standard F test for unequal variances is also performed. The F test is the ratio of the larger to the smaller variance estimate. The p-value from the F distribution is doubled to make it a two-sided test.
Note: If you have specified a Block column, then the variance tests are performed on data after it has been adjusted for the Block means.