Variance Components
The Variance Components option models the variation from measurement to measurement. The response is assumed to be a constant mean plus random effects associated with various levels of the classification.
Note: Once you select the Variance Components option, if you did not select the Model Type in the launch window (if you selected Decide Later), you are prompted to select the model type. For more information about model types, see Launch the Variability/Attribute Gauge Chart Platform.
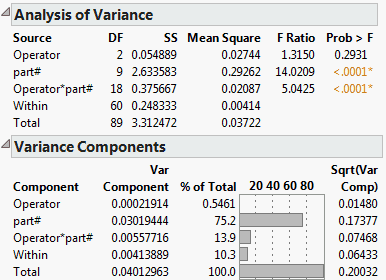
Figure 5.5 Example of the Variance Components Report
The Analysis of Variance report appears only if the EMS method of variance component estimation is used. This report shows the significance of each effect in the model.
The Variance Components report shows the estimates themselves. See Statistical Details for Variance Components.
Analysis Settings
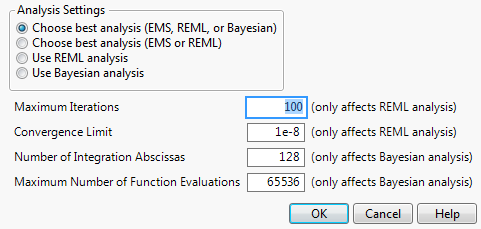
From the launch window, click Analysis Settings to choose the method for computing variance components.
Figure 5.6 Analysis Settings Window
Choose best analysis (EMS, REML, or Bayesian)
Chooses the best analysis from EMS, REML, or Bayesian, using the following logic:
– If the data are balanced, and if no variance components are negative, the EMS (expected mean squares) method is used to estimate the variance components.
– If the data are unbalanced, the REML (restricted maximum likelihood) method is used, unless a variance component is estimated to be negative, then the Bayesian method is used.
– If any variance component is estimated to be negative using the EMS method, the Bayesian method is used.
– If there is confounding in the variance components, then the bounded REML method is used, and any negative variance component estimates are set to zero.
Choose best analysis (EMS or REML)
Chooses the best analysis from EMS or REML, using the same logic as the Choose best analysis (EMS, REML, or Bayesian) option. However, this option never uses the Bayesian method, even for negative variance components. The bounded REML method is used and any negative variance component is forced to be 0.
Use REML analysis
Uses the bounded REML method, even if the data are balanced. The bounded REML method can handle unbalanced data and forces any negative variance component to be 0.
Use Bayesian analysis
Uses the Bayesian method. The Bayesian method can handle unbalanced data and forces all variances components to be positive and nonzero. If there is confounding in the variance components, then the bounded REML method is used, and any negative variance component estimates are set to zero. The method implemented in JMP computes the posterior means using a modified version of Jeffreys’ prior. See Portnoy (1971) and Sahai (1974).
Maximum Iterations
(Applicable only for the REML method.) For difficult problems, you might want to increase the number of iterations. Increasing this value means that JMP will try more times to find a solution in the optimization phase.
Convergence Limit
(Applicable only for the REML method.) For problems where you want greater precision, you might want to change the convergence limit to be smaller. Decreasing this value means that JMP will find the solution to a higher level of accuracy in the optimization phase. However, this can increase the time taken to find a solution. Providing a larger convergence value returns quicker results, but is less precise.
Number of Iteration Abscissas
(Applicable only for the Bayesian method.) For greater accuracy, you might want to increase the number of iteration abscissas. However, this can increase the time taken to find a solution. Providing a smaller number returns quicker results, but is less precise.
Maximum Number of Function Evaluations
(Applicable only for the Bayesian method.) For greater accuracy, you might want to increase the maximum number of function evaluations. However, this can increase the time taken to find a solution. Providing a smaller number returns quicker results, but is less precise.