Computations for the Power
Suppose that you are interested in computing the power of a test of a linear hypothesis, based on significance level α and a sample size of N. You want to detect an effect of size δ.
To calculate the power, begin by finding the critical value for an α-level F test of the linear hypothesis. This is given by solving for FC in the equation

Here, dfHyp represents the degrees of freedom for the hypothesis, dfModel represents the degrees of freedom for the model, and N is the proposed (or actual) sample size.
Then calculate the noncentrality parameter associated with the desired effect size. The noncentrality parameter is defined as follows:
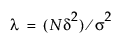
where σ2 is a proposed (or estimated) value of the error variance.
Given an effect of size δ, the test statistic has a non-central F distribution, where the distribution function is denoted FDist below, with noncentrality parameter λ. To obtain the power of your test, calculate the probability that the test statistic exceeds the critical value:
Power = 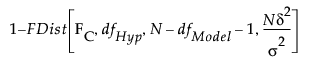
In obtaining retrospective power for a study with n observations, JMP estimates the noncentrality parameter λ = (nδ2)/σ2 by 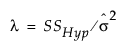 , where SSHyp represents the sum of squares due to the hypothesis.
, where SSHyp represents the sum of squares due to the hypothesis.