Example of Nominal Logistic Regression
An experiment was performed on metal ingots that were prepared with different heating and soaking times and then tested for readiness to roll. See Cox and Snell (1989). The data are contained in the Ingots.jmp sample data table. In this example, the Fit Model platform fits the probability of the Ready response using a logistic regression model with regressors heat and soak.
1. Select Help > Sample Data Library and open Ingots.jmp.
The values of the categorical variable ready, Ready and Not Ready, indicate whether an ingot is ready to roll.
2. Select Analyze > Fit Model.
3. Select ready and click Y.
Because you selected a column with the Nominal modeling type, the Fit Model Personality updates to Nominal Logistic.
Because ready is a Nominal column with only two levels, the Target Level option appears. This option enables you to specify the response level whose probability you want to model.
4. From the Target Level list, select Ready.
In this model, the Target Level is Ready, so you are modeling the probability of the Ready response.
5. Select heat and soak and click Add.
6. Select count and click Freq.
7. Click Run.
When the fitting process converges, the nominal regression report appears.
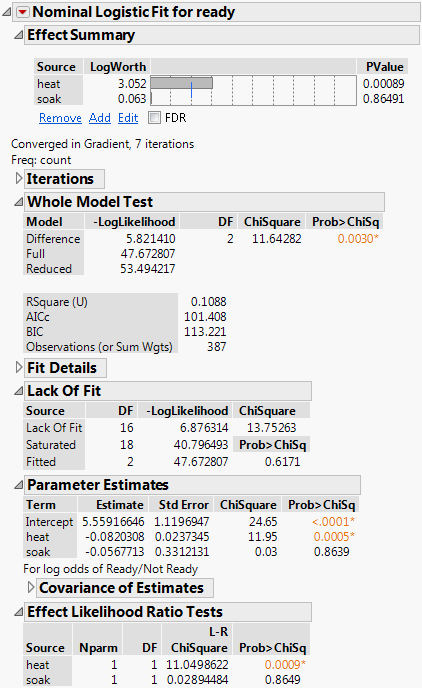
Figure 11.2 Nominal Logistic Fit Report
In the Whole Model Test report, the chi-square statistic (11.64) has a small p-value (0.0030), which indicates that the overall model is significant. However, the parameter estimate for soak has a p-value of 0.8639, which indicates that soaking time is not statistically significant.
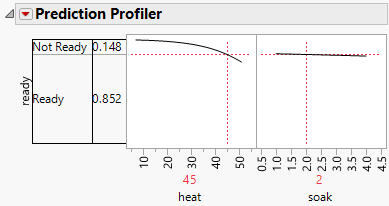
8. Click the red triangle next to Nominal Logistic Fit for ready and select Profiler.
Figure 11.3 Prediction Profiler
When heat is set at 45 and soak is set at 2 the probability of ready is 0.85.
At this point, you might also be interested in using inverse prediction to find the heating time at a specific soaking time and given a particular probability of readiness to roll. See Example of Inverse Prediction for a continuation of this example.