Fit Parametric Survival
Fit Survival Data Using Regression Models
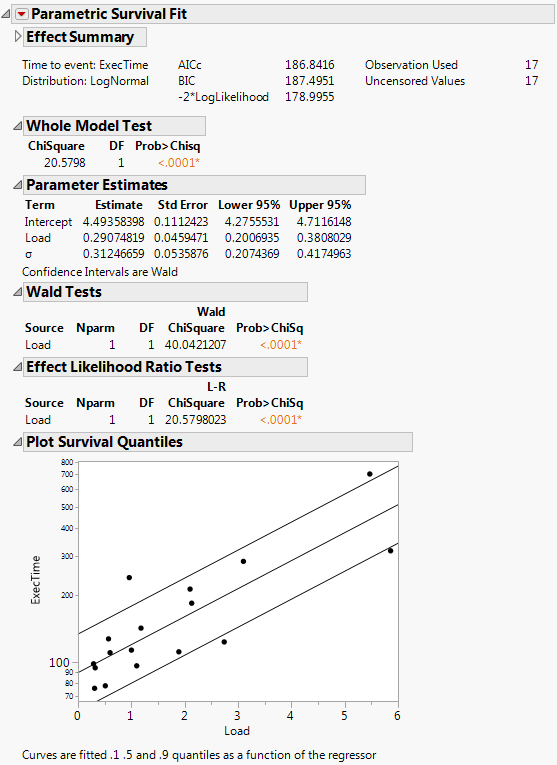
Survival times can be expressed as a function of one or more variables. When this is the case, use a regression platform that fits a linear regression model while taking into account the survival distribution and censoring. The Fit Parametric Survival platform fits the time to event Y (with censoring) using linear regression models that can involve both location and scale effects. The fit is performed using the Weibull, lognormal, exponential, Fréchet, loglogistic, smallest extreme value (SEV), normal, largest extreme value (LEV), and logistic distributions.
Note: The Fit Parametric Survival platform is a slightly customized version of the Fit Model platform. You can also fit parametric survival models using the Nonlinear platform.
Figure 14.1 Example of a Parametric Survival Fit