Kolmogorov-Smirnov Two-Sample Test Report
The Kolmogorov-Smirnov test is available only when X has exactly two levels. The report shows descriptive statistics followed by test results. The descriptive statistics are the following:
Level
The two levels of X.
Count
The frequencies of each level.
EDF at Maximum
For a level of X, gives the value of the empirical cumulative distribution function (EDF) for that level at the value of X for which the difference between the two EDFs is a maximum. For the row named Total, gives the value of the pooled EDF (the EDF for the entire data set) at the value of X for which the difference between the two EDFs is a maximum.
Deviation from Mean at Maximum
For each level, gives the value obtained by the following steps:
– Compute the difference between the EDF at Maximum for the given level and the EDF at maximum for the pooled data set (Total).
– Multiply this difference by the square root of the number of observations in that level, given as Count.
Kolmogorov-Smirnov Asymptotic Test
This report gives the details for the test.
KS
A Kolmogorov-Smirnov statistic computed as follows:
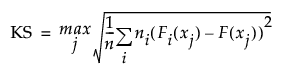
The formula uses the following notation:
– xj, j = 1,..., n are the observations
– ni is the number of observations in the ith level of X
– F is the pooled cumulative empirical distribution function
– Fi is the cumulative empirical distribution function for the ith level of X
This version of the Kolmogorov-Smirnov statistic applies even when there are more than two levels of X. Note, however, that JMP performs the Kolmogorov-Smirnov analysis only when X has only two levels of X.
KSa
An asymptotic Kolmogorov-Smirnov statistic computed as 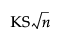 , where n is the total number of observations.
, where n is the total number of observations.
D=max|F1-F2|
The maximum absolute deviation between the EDFs for the two levels. This is the version of the Kolmogorov-Smirnov statistic typically used to compare two samples.
Prob > D
The p-value for the test. This is the probability that D exceeds the computed value under the null hypothesis of no difference between the levels.
D+ = max(F1-F2)
A one-sided test statistic for the alternative hypothesis that the level of the first group exceeds the level of the second group.
Prob > D+
The p-value for the test of D+.
D- = max(F2-F1)
A one-sided test statistic for the alternative hypothesis that the level of the second group exceeds the level of the first group
Prob > D-
The p-value for the test of D-.
 Kolmogorov-Smirnov Exact Test
Kolmogorov-Smirnov Exact Test
For the Kolmogorov-Smirnov exact test, the report gives the same statistics as does the asymptotic test, but the p-values are computed to be exact.