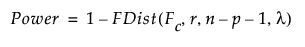Power for a Categorical Effect
This section describes how power for the test for a whole categorical effect is computed. Use the following notation:
X
Model matrix. See The Alias Matrix.
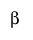
Vector of parameters.
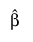
Least squares estimate of β.
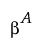
Vector of Anticipated Coefficient values.
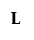
Matrix that defines the test for the categorical effect. The matrix L identifies the values of the parameters in β corresponding to the categorical effect and sets them equal to 0. The null hypothesis for the test of the categorical effect is given by:
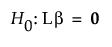
r
Rank of L. Alternatively, r is the number of levels of the categorical effect minus one.
Note: You can view the design matrix by running Fit Model. Then select Save Columns > Save Coding Table from the red triangle menu for the main report.
The covariance matrix of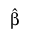 
is given by 
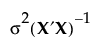, where σ2 is the error variance.
The error variance, σ2, is estimated by the MSE, and has n − p − 1 degrees of freedom, where n is the number of observations and p is the number of terms other than the intercept in the model. If n − p − 1 = 0, then JMP sets the degrees of freedom for the error to 1. This allows the power to be estimated for parameters in a saturated design.
The test of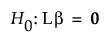 
is given by:
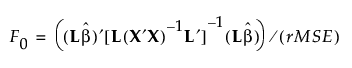
Under the null hypothesis, the test statistic F0 has an F distribution on r and n − p − 1 degrees of freedom.
If the true value of β is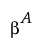 
, then F0 has a noncentral F distribution with noncentrality parameter given by:
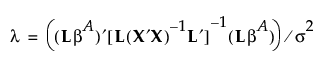
To compute the power of the test, first solve for the α-level critical value Fc:
Then calculate the power as follows:
