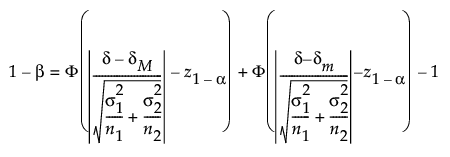Power for Two Independent Sample Equivalence
Use the Power Explorer for Two Sample Equivalence to determine a sample size for an equivalence test of two groups. Select DOE > Sample Size Explorers > Power > Power for Two independent Sample Equivalence. Explore the trade offs between variability assumptions, sample size, power, significance, and the equivalence range. Sample size and power are associated with the following hypothesis test:
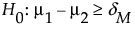 or
or 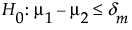
versus the alternative:
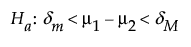
where μ1 and μ2 the true group means and (δm, δM) is the equivalence range. For the same significance level and power, a larger sample size is needed to detect a small difference than to detect a large difference. It is assumed that the populations of interest are normally distributed.
Power Explorer for Two Independent Sample Equivalence Options
Set study assumptions and explore sample sizes using the radio buttons, text boxes, and sliders. The curve updates as you make changes to the settings. Alternatively, change settings by dragging the cross hairs on the curve or adjusting the values in the axis text boxes.
Equivalence Range
Maximum difference
Specifies the margin above which the mean is considered different from the reference mean
Minimum difference
Specifies the margin below which the mean is considered different from the reference mean.
Note: Typically, the equivalence margin is symmetric. However, it does not have to be symmetric.
Fixed Parameters
Alpha
Specifies the probability of a type I error, which is the probability of rejecting the null hypothesis when it is true. It is commonly referred to as the significance level of the test. The default alpha level is 0.05.
Group 1 StdDev (σ1)
Specifies the assumed population standard deviation for one of your groups, Group 1.
Group 2 StdDev (σ2)
Specifies the assumed population standard deviation for the second group, Group 2.
Population standard deviations known
Specifies calculations based on a known, rather than assumed, population standard deviations.
Test Parameters
Parameters that are inter-related and update as you make changes.
Difference in Means
Specifies the difference between group means that defines the equivalence range.
Group 1 Sample Size
Specifies the number of observations (runs, experimental units, or samples) needed for Group 1 in your experiment. Select Lock to lock the Group 1 sample size.
Group 2 Sample Size
Specifies the number of observations (runs, experimental units, or samples) needed for Group 2 in your experiment. Select Lock to lock the Group 2 sample size.
Total Sample Size
Specifies the total number of observations (runs, experimental units, or samples) needed for your experiment. The power curve is based on total sample size. Select Lock to lock the total sample size.
Note: Adjusting the sample size for one group adjusts the total sample size unless the total sample size is locked. In that case, adjusting the sample size for one group adjust the sample size for the second group. Adjusting the total sample size adjusts the two groups proportionally, unless one group is locked. Use only one lock at a time.
Power
Specifies the probability of rejecting the null hypothesis when it is false. With all other parameters fixed, power increases as sample size increases.
Save Settings
Saves the current settings to the Saved Settings table. This enables you to save a set of alternative study plans. See Saved Settings in the Sample Size Explorers.
Make Data Collection Table
Creates a new data table that you can use for data collection.
Statistical Details for the Two Independent Sample Equivalence Explorer
The power calculations for testing equivalence of two group means is based on methods described in Chow et al. (2008).
If σ1 and σ2 are unknown, the power (1-β) is computed as follows:
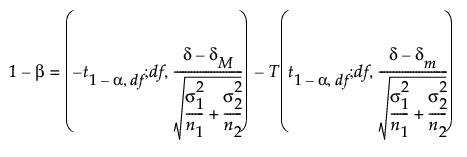
where:
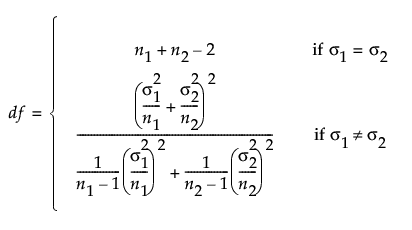
α is the significance level
n1 and n2 are the group sample sizes
σ1 and σ2 are the assumed group standard deviations
δ is the difference to detect
(δm, δM) is the equivalence range
t1-α,ν,is the (1 - α)th quantile of the central t-distribution with ν degrees of freedom
T(t; ν, λ) is the cumulative distribution function of the non-central t distribution with ν degrees of freedom and non-centrality parameter λ.
If σ is known, then power (1-β) is computed as follows: