 Statistical Details for Estimation Methods
Statistical Details for Estimation Methods
Penalized regression methods introduce bias to the regression coefficients by penalizing them.
 Ridge Regression
Ridge Regression
An l2 penalty is applied to the regression coefficients during ridge regression. Ridge regression coefficient estimates are defined as follows:
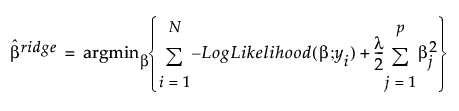 ,
,
where 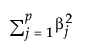 is the l2 penalty, λ is the tuning parameter, N is the number of rows, and p is the number of variables.
is the l2 penalty, λ is the tuning parameter, N is the number of rows, and p is the number of variables.
 Dantzig Selector
Dantzig Selector
An l∞ penalty is applied to the regression coefficients during Dantzig Selector. Coefficient estimates for the Dantzig Selector satisfy the following criterion:
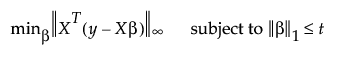
where 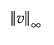 denotes the l∞ norm, which is the maximum absolute value of the components of the vector v.
denotes the l∞ norm, which is the maximum absolute value of the components of the vector v.
 Lasso Regression
Lasso Regression
An l1 penalty is applied to the regression coefficients during Lasso. Coefficient estimates for the Lasso are defined as follows:
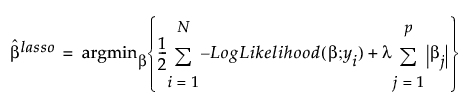 ,
,
where 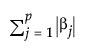 is the l1 penalty, λ is the tuning parameter, N is the number of rows, and p is the number of variables
is the l1 penalty, λ is the tuning parameter, N is the number of rows, and p is the number of variables
 Elastic Net
Elastic Net
The Elastic Net combines both l1 and l2 penalties. Coefficient estimates for the Elastic Net are defined as follows:
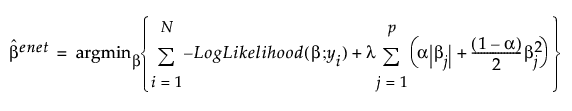 ,
,
This is the notation used in the equation:
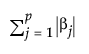 is the l1 penalty
is the l1 penalty
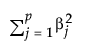 is the l2 penalty
is the l2 penalty
λ is the tuning parameter
α is a parameter that determines the mix of the l1 and l2 penalties
N is the number of rows
p is the number of variables
Tip: There are two sample scripts that illustrate the shrinkage effect of varying α and λ in the Elastic Net for a single predictor. Select Help > Sample Data, click Open the Sample Scripts Directory, and select demoElasticNetAlphaLambda.jsl or demoElasticNetAlphaLambda2.jsl. Each script contains a description of how to use it and what it illustrates.
 Adaptive Methods
Adaptive Methods
The adaptive Lasso method uses weighted penalties to provide consistent estimates of coefficients. The weighted form of the l1 penalty is defined as follows:
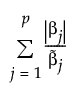
where 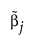 is the MLE when the MLE exists. If the MLE does not exist and the response distribution is normal, estimation is done using least squares and
is the MLE when the MLE exists. If the MLE does not exist and the response distribution is normal, estimation is done using least squares and 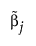 is the solution obtained using a generalized inverse. If the response distribution is not normal,
is the solution obtained using a generalized inverse. If the response distribution is not normal, 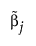 is the ridge solution.
is the ridge solution.
For the adaptive Lasso, this weighted form of the l1 penalty is used in determining the 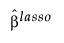 coefficients.
coefficients.
The adaptive Elastic Net uses this weighted form of the l1 penalty and also imposes a weighted form of the l2 penalty. The weighted form of the l2 penalty for the adaptive Elastic Net is defined as follows:
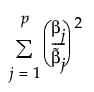
where 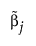 is the MLE when the MLE exists. If the MLE does not exist and the response distribution is normal, estimation is done using least squares and
is the MLE when the MLE exists. If the MLE does not exist and the response distribution is normal, estimation is done using least squares and 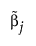 is the solution obtained using a generalized inverse. If the response distribution is not normal,
is the solution obtained using a generalized inverse. If the response distribution is not normal, 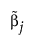 is the ridge solution.
is the ridge solution.