Statistical Details for the EWMA Control Chart Platform
This section defines the statistics that are used in the construction of the EWMA chart. Some of these statistics are also saved in the data table that is created by the Save Summaries command.
The ith point on the EWMA chart is calculated as follows:
EWMAi = λXi + (1 - λ)EWMAi-1
where:
λ = Lambda parameter
Xi = ith sample value (or subgroup mean)
EWMAi-1 = (i-1)th EWMA value
When i = 1, define EWMA0 as the Target value.
Note: When the Restart EWMA after Empty Subgroup option is selected, the EWMAi-1 value following an empty subgroup is the Target value. When the Restart EWMA after Empty Subgroups option is not selected, the EWMAi-1 value following an empty subgroup is the EWMA value for the most recent non-empty subgroup.
The computation of the control limits on the EWMA chart is determined by the setting of the Constant Limits option.
EWMA Limits
When the Constant Limits option is not selected and the subgroup sizes are not equal, the EWMA control limits are computed as follows:
LCL = 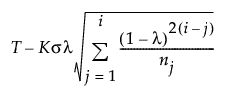
UCL = 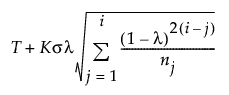
where:
T = Target value
K = the sigma multiplier and is set to 3 by default
σ = Sigma value
i = the number of the sample (or subgroup)
ni = the size of subgroup i
When the Constant Limits option is not selected and the subgroup sizes are equal, the formulas for the EWMA control limits simplify as follows:
LCL = 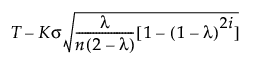
UCL = 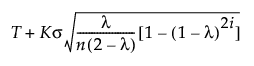
where:
T = Target value
K = the sigma multiplier and is set to 3 by default
σ = Sigma value
i = the number of the sample (or subgroup)
n = the size of each subgroup (or 1 if no subgroup is specified)
Constant Limits
When the Constant Limits option is selected, the EWMA control limits are computed as follows:
LCL = 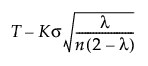
UCL = 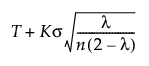
where:
T = Target value
K = the sigma multiplier and is set to 3 by default
σ = Sigma value
n = the subgroup size (or 1 if no subgroup is specified)
For more information about constructing exponentially weighted moving average charts, see Montgomery (2013).