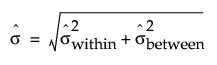Variation Statistics
Denote the standard deviation of the process by σ. The Process Capability platform provides two types of capability indices. The Ppk indices are based on an estimate of σ that uses all of the data in a way that does not depend on subgroups. This overall estimate can reflect special cause as well as common cause variation. The Cpk indices are based on an estimate that attempts to capture only common cause variation. The Cpk indices are constructed using within-subgroup or between-and-within-subgroup estimates of σ. In this way, they attempt to reflect the true process standard deviation. When a process is not stable, the different estimates of σ can differ markedly.
Overall Sigma
The overall sigma does not depend on subgroups. The overall estimate of σ is calculated as follows:
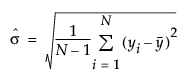
The formula uses the following notation:
N = number of nonmissing values in the entire data set
yi = value of the ith observation
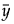 = mean of nonmissing values in the entire data set
= mean of nonmissing values in the entire data set
Caution: When the process is stable, the Overall Sigma estimates the process standard deviation. If the process is not stable, the overall estimate of σ is of questionable value, since the process standard deviation is unknown.
Estimates of Sigma Based on Within-Subgroup Variation
An estimate of σ that is based on within-subgroup variation can be constructed in one of the following ways:
• Within sigma estimated by average of ranges
• Within sigma estimated by average of unbiased standard deviations
• Within sigma estimated by moving range
• Within sigma estimated by unbiased pooled standard deviation
If you specify a subgroup ID column or a constant subgroup size on the launch window, you can specify your preferred within-subgroup variation statistic. See Launch the Process Capability Platform. If you do not specify a subgroup ID column, a constant subgroup size, or a historical sigma, JMP estimates the within sigma using the third method (moving range of subgroups of size two).
Within Sigma Based on Average of Ranges
Within sigma estimated by the average of ranges is the same as the estimate of the standard deviation of an XBar and R chart:
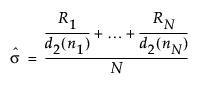
The formula uses the following notation:
Ri = range of ith subgroup
ni = sample size of ith subgroup
d2(ni) = expected value of the range of ni independent normally distributed variables with unit standard deviation
N = number of subgroups for which ni ≥ 2
Within Sigma Based on Average of Unbiased Standard Deviations
Within sigma estimated by the average of unbiased standard deviations is the same as the estimate for the standard deviation in an XBar and S chart:
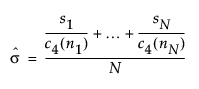
The formula uses the following notation:
ni = sample size of ith subgroup
c4(ni) = expected value of the standard deviation of ni independent normally distributed variables with unit standard deviation
N = number of subgroups for which ni ≥ 2
si = sample standard deviation of the ith subgroup
Within Sigma Based on Average Moving Range
Within sigma estimated by average moving range is the same as the estimate for the standard deviation for Individual Measurement and Moving Range charts:
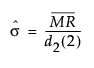
The formula uses the following notation:
 = the mean of the nonmissing moving ranges computed as (MR2+MR3+...+MRN)/(N-1) where MRi = |yi - yi-1|.
= the mean of the nonmissing moving ranges computed as (MR2+MR3+...+MRN)/(N-1) where MRi = |yi - yi-1|.
d2(2) = expected value of the range of two independent normally distributed variables with unit standard deviation.
Within Sigma Based on Median Moving Range
Within sigma estimated by median moving range:
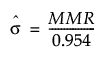
The formula uses the following notation:
MMR = the median of the nonmissing moving ranges computed as Median(MR2, MR3,..., MRN) where MRi = |yi - yi-1|.
Within Sigma Based on Unbiased Pooled Standard Deviation
Within sigma estimated by the unbiased pooled standard deviation:
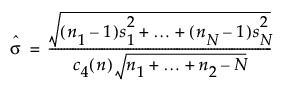
The formula uses the following notation:
ni = sample size of ith subgroup
n = n1 + … + nN, the total sample size
c4(n) = expected value of the standard deviation of n independent normally distributed variables with unit standard deviation
N = number of subgroups for which ni ≥ 2
si = sample standard deviation of the ith subgroup
Estimate of Sigma Based on Between Group Variation
Between Sigma Based on Moving Range
The estimate of σ that is based on between-subgroup variation is estimated by the moving range of subgroup means:
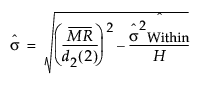
The formula uses the following notation:
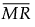 = the mean of the nonmissing moving ranges computed as (MR2+MR3+...+MRN)/(N-1) where MRi = |yi - yi-1|.
= the mean of the nonmissing moving ranges computed as (MR2+MR3+...+MRN)/(N-1) where MRi = |yi - yi-1|.
d2(2) = expected value of the range of two independent normally distributed variables with unit standard deviation.
σ2within = the specified within sigma estimate.
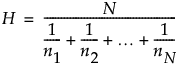 , the harmonic mean of subgroup sample sizes.
, the harmonic mean of subgroup sample sizes.
Estimate of Sigma Based on Between and Within Group Variation
Between-and-Within Sigma
The estimate of sigma that is based on the combined between and within group variation is defined as follows: