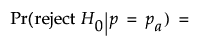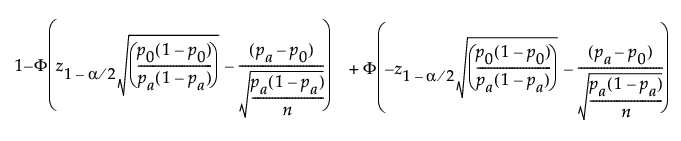Power for One Sample Proportion
Use the Power for One Sample Proportion Explorer to determine a sample size for a hypothesis test about one proportion. Select DOE > Sample Size Explorers > Power > Power for One Sample Proportion. Explore the trade-offs between sample size, power, significance, and the hypothesized difference to detect. Sample size and power are associated with the following hypothesis test:
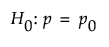
versus the two-sided alternative:
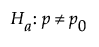
or versus a one-sided alternative:
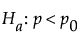 or
or 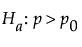
where p is the population proportion and p0 is the null proportion.
Power Explorer for One Sample Proportion Settings
Set study assumptions and explore sample sizes by using the radio buttons, text boxes, and menus. The profiler updates as you make changes to the settings. Alternatively, you can change the settings by dragging the cross hairs on the profiler curves.
Test Type
Specifies a one- or two-sided hypothesis test.
Alpha
Specifies the probability of a type I error, which is the probability of rejecting the null hypothesis when it is true. It is commonly referred to as the significance level of the test. The default alpha level is 0.05.
Test Method
Exact Test
Specifies calculations based on the Clopper-Pearson methodology.
Normal Approximation
Specifies calculations based on the normal approximation methodology.
Tip: Since the binomial distribution is discrete, the actual test size can differ significantly from the stated Alpha level for small samples or proportions near 0 or 1. To guarantee an alpha level equal to or greater than your stated level, use the Exact test.
Power Explorer for One Sample Proportion Profiler
The profiler enables you to visualize the impact of sample size assumptions on the power calculations. Interactive profiler changes to the sample size, assumed proportion, or alternative proportion update the calculated power. Interactive changes to the profiler power update the sample size. To solve for a specific variable, use the target variable setting and click Go.
Target Variable
Enables you to solve for sample size, assumed proportion, or the alternative proportion at a specified power.
Power
Specifies the probability of rejecting the null hypothesis when it is false. With all other parameters fixed, power increases as sample size increases.
Sample Size
Specifies the total number of observations (runs, experimental units, or samples) that are needed for your experiment.
Note: When the exact method is used, the profile for sample size is a nonmonotonic function. This is due to the limited number of values that the test statistic can take. A proportion for a fixed sample size can take on only a fixed number of values. This behavior is especially noticeable for small sample sizes and small differences to detect. In practice, explore both the exact and normal approximation sample size estimates and select a sample size to appropriate for the risk profile of your study.
Assumed proportion
Specifies the proportion that you anticipate or assume for your study, the null hypothesis value, which is often denoted as p0.
Alternative proportion
Specifies the proportion that you test against, the alternative hypothesis value, which is often denoted as pA.
Power Explorer for One Sample Proportion Options
The Explorer red triangle menu and report buttons provide additional options:
Simulate Data
Opens a data table of simulated data that are based on the explorer settings. View the simulated response column formula for the settings that are used. Run the table script to analyze the simulated data.
Make Data Collection Table
Creates a new data table that you can use for data collection. The table includes scripts to facilitate data analysis.
Remember Settings
Saves the current settings to the Remembered Settings table. This enables you to save a set of alternative study plans. See Remembered Settings in the Sample Size Explorers.
Reset to Defaults
Resets all parameters and graphs to their default settings.
The Profiler red triangle menu contains the following option:
Optimization and Desirability
Enables you to optimize settings. See “Desirability Profiling and Optimization” in Profilers.
Note: The sample size explorer report can be saved as a *.jmpdoe file. Open the file to return to the explorer. An alert prompts you to save the file.
Example of Power Explorer for One Sample Proportion
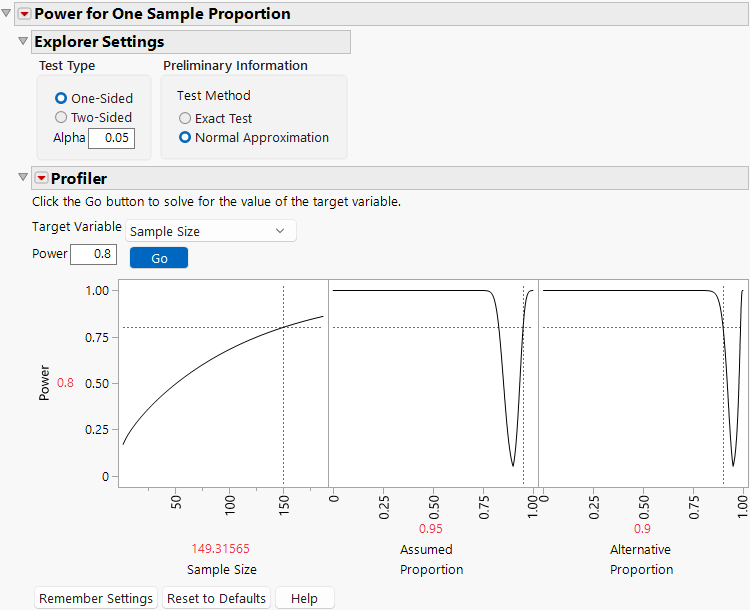
In this example, use the Power Explorer for One Sample Proportion to help determine the number of samples to test to demonstrate a process success rate of least 90%. You would like your study to have at least 80% power to demonstrate a success rate of at least 90% assuming that you achieve a success rate of at least a 95% at a significance level of α = 0.05. You use a one-sided test using the normal approximation methodology.
1. Select DOE > Sample Size Explorers > Power > Power for One Sample Proportion.
2. Select One-Sided for Test Type.
3. Leave Alpha set to 0.05.
4. Select Normal Approximation for Test Method.
5. Leave Target Variable set to Sample Size.
6. Leave Power set to 0.8.
7. In the profiler, use the slider or click on the red value for a text box to set the Assumed Proportion to 0.95. This is the proportion you assume that you can achieve.
8. In the profiler, set the Alternative Proportion to 0.90. This is the minimum proportion that you want to demonstrate that your process can achieve.
9. Click Go.
Figure 29.3 One Sample Proportion Explorer
Note that a sample size of 150 is needed to show that an expected success rate of 95% is greater than 90% with 80% power using a one-sided test of proportions using the normal approximation methodology.
Statistical Details for the Power Explorer for One Sample Proportion
For the exact test, the power is computed based on the form of the alternative hypothesis.
For one-sided, higher alternative:
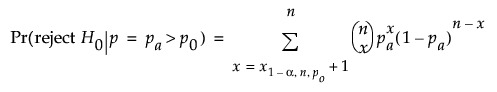
for a one-sided, lower alternative:
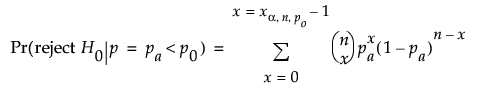
for a two-sided alternative:
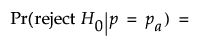
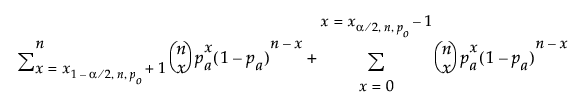
where xq,n,p is the qth quantile of a binomial distribution with n trials and probability p.
Notes:
• The floor function is used for the exact method, providing the minimum sample size that is needed for the specified inputs.
• When solving for power, for a given sample size and assumed probability, there can be a range of powers that satisfy the discrete binomial equation. The power closest to the target is provided.
For the normal approximation, the power is computed based on the form of the alternative hypothesis.
For a one-sided, higher alternative:
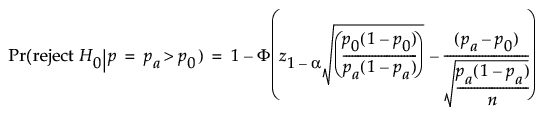
For a one-sided, lower alternative:
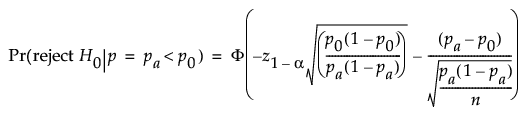
For a two-sided alternative: