 Statistical Details for Causal Assumptions
Statistical Details for Causal Assumptions
The Causal Treatment personality allows for the estimation of causal quantities. A causal quantity is a function of potential outcomes. A potential outcome is a value that would be observed if the treatment variable X were set to a given value x. For example, in the case of a binary treatment X and an outcome of interest Y, each individual has two potential outcomes: Y(0) and Y(1). However, in a data set, only one of these values might be observable at a given time for a given observation, if at all.
In a randomized controlled trial, treatment is randomly assigned, balancing the different treatment groups on all variables aside from the treatment itself. However, in observational studies, there is often a set of confounding variables Z that affect both the treatment and the outcome. Causal inference methods are used to control for this confounding bias and to estimate potential outcomes by leveraging information from a given sample.
Three assumptions are needed to identify causal quantities of interest from observational data. Aside from positivity, these assumptions cannot be tested empirically using a given data set, because they are assumptions about the data-generating process rather than the given sample.
The following are the three properties one must assume to draw causal conclusions from observational data:
1. Positivity
2. Consistency
3. Conditional exchangeability
Positivity
Positivity assumes that, for all combination of values of Z, there is a positive probability of receiving each treatment level. This can be written equivalently as the following formula:
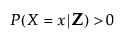
for each x of interest.
Consistency
Consistency assumes that each observation that receives treatment level x receives the exact same intervention. Therefore, X is well-defined, and observing the value that Y takes when the treatment level has been set to x is the same as observing the potential outcome Y(x) for every individual in the sample. This can be written equivalently as the following equation:
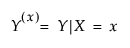
for every observation with X = x.
Conditional Exchangeability
Conditional exchangeability assumes that the probability of being assigned treatment depends only on measured confounders Z. In other words, Y(x) is independent of X|Z, where Z is the set of variables that confound the effect of X on Y.