Statistical Details for Change Point Detection
This section contains details for the Change Point Detection option in the Multivariate Control Chart platform. This discussion follows the development in Sullivan and Woodall (2000).
Assumptions
Denote a multivariate distribution of dimension p with mean vector μi and covariance matrix Σi by Np(μi,Σi). Suppose that the xi are m (where m > p) independent observations from such a distribution:
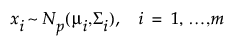
If the process is stable, the means μi and the covariance matrices Σi equal a common value so that the xi have a Np(μ, Σ) distribution.
Suppose that a single change occurs in either the mean vector or the covariance matrix, or both, between the m1 and m1+1 observations. Then the following conditions hold:
• Observations 1 through m1 have the same mean vector and the same covariance matrix (μa,Σa).
• Observations m1 + 1 to m have the same mean vector and covariance matrix (μb,Σb).
• One of the following occurs:
– If the change affects the mean, μa ≠ μb.
– If the change affects the covariance matrix, Σa ≠ Σb.
– If the change affects both the mean and the covariance matrix, μa ≠ μb and Σa ≠ Σb.
Overview
A likelihood ratio test approach is used to identify changes in one or both of the mean vector and covariance matrix. The likelihood ratio test statistic is used to compute a control chart statistic that has an approximate upper control limit of 1. The control chart statistic is plotted for all possible m1 values. If any observation’s control chart statistic exceeds the upper control limit of 1, this is an indication that a shift occurred. Assuming that exactly one shift occurs, that shift is considered to begin immediately after the observation with the maximum control chart statistic value.