Statistical Details for Continuous Treatment Methods
There are two methods in the Causal Treatment personality that are used to estimate mean potential outcomes when the treatment is continuous. One method is Marginal Structural Modeling (MSM) with inverse probability weighting with ratio adjustment (IPWR) and the other method is Generalized Propensity Score (GPS) modeling. The MSM method comes from Hernán and Robins (2020) and the GPS method comes from Hirano and Imbens (2005).
Both methods involve estimating a propensity score using probability density functions. In the Causal Treatment personality, the density f(X|Z) is assumed to be normal with mean E[X|Z] and variance σ2. These parameters are estimated using linear regression. Then, the generalized propensity score, Ri, for observation i is defined as follows:
.
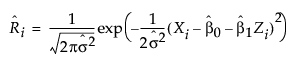The methods then differ in how this propensity score is used.
Marginal Structural Modeling with IPWR
The Causal Treatment personality uses the MSM method as described in Hernán and Robins (2020). An MSM models the marginal mean of the potential outcome at a given level of the treatment x. In the Causal Treatment personality, the MSM is assumed to be of the following form:
.
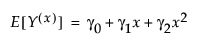The γ parameters are estimated using linear regression with stabilized inverse probability weights. When the treatment is continuous, stabilized weights are defined as follows:
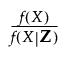
where f(X) is the marginal probability density function of X and f(X|Z) is the conditional probability density function of X|Z. The marginal density is modeled using a null linear regression model with the treatment X as the outcome and no predictors. The conditional density is modeled as described above.
Once estimates for the parameters are found through weighted linear regression, mean potential outcomes are estimated by plugging in specified values of the treatment.
Generalized Propensity Score Modeling
The Causal Treatment personality uses the GPS method as described in Hirano and Imbens (2005). The GPS method works by estimating a generalized propensity score and using it as an effect in modeling the outcome Y.
A linear regression is fit to model the outcome Y, which is assumed to take the following form:
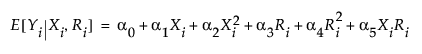
where the R2 term is calculated after centering.
Once the linear regression is fit, the parameter estimates are used to calculate the mean potential outcome at the treatment level x as follows:
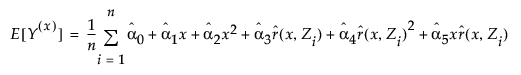
where r(x, Zi) is the generalized propensity score, as denoted above, for observation i at treatment level x.