Statistical Details for Tolerance Intervals
This section contains statistical details for one-sided and two-sided tolerance intervals in the Distribution platform.
Normal Distribution-Based Tolerance Intervals
One-Sided Interval
The one-sided interval is computed as follows:
Lower Limit = 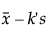
Upper Limit = 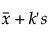
where
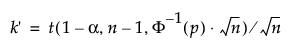
s is the standard deviation
t is the quantile from the noncentral t-distribution
Φ-1 is the standard normal quantile
Two-Sided Interval
The two-sided interval is computed as follows:
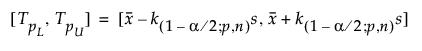
where s is the standard deviation and k(1-α/2; p,n) is a constant.
To determine k, consider the fraction of the population captured by the tolerance interval. Tamhane and Dunlop (2000) define this fraction as follows:
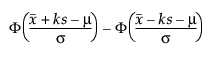
where Φ denotes the standard normal cdf (cumulative distribution function).
Therefore, k solves the following equation:
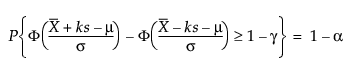
where 1 - γ is the fraction of all future observations contained in the tolerance interval.
For more information about normal distribution-based tolerance intervals, see Tables J.1a, J.1b, J.6a, and J.6b of Meeker et al. (2017).
Nonnormal Distribution-Based Tolerance Intervals
Lognormal
Tolerance intervals for data that follow a lognormal distribution are computed by taking the log of the data to transform to normally distributed data. The tolerance interval is then calculated assuming normality and exponentiated to transform back to the lognormal scale.
Gamma
Tolerance intervals for data distributed gamma(a, b) are computed by taking the cube root of the data to transform to normally distributed data. The tolerance interval is then calculated assuming normality with mean and variance defined by:
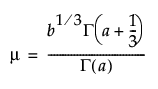
and
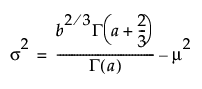
where Γ(.) is the gamma function and a and b are the shape and scale parameters of the gamma distribution of the data. Once calculated, the tolerance interval is then cubed to transform back to the gamma scale. For more information about tolerance intervals for Gamma distributed data see Krishnamoorthy et. al. (2008).
Exponential
The calculations for tolerance intervals based on an exponential distribution are dependent on the type of interval.
A one sided (1-α, p) lower tolerance limit is calculated as:
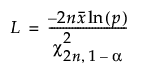
A one sided (1-α, p) upper tolerance limit is calculated as:
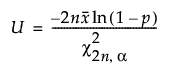
Two-sided tolerance intervals are obtained by solving a system of three non-linear equations. See Fernandez (2010).
Weibull, SEV, and LEV
Tolerance intervals for the smallest extreme value (SEV) distribution are calculated using the methods of Lawless (1975).
Tolerance intervals based on a Weibull distribution are computed by transforming the data to a SEV distribution, calculating the tolerance interval, and then transforming back to a Weibull distribution.
A Weibull (b, c) distribution is related to the SEV(0, 1) distribution by
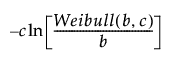
Tolerance intervals based on the Largest Extreme Value (LEV) distribution are computed using the SEV intervals. One negates the data to transform to SEV data. Calculate the intervals and then transform back to LEV. Two sided tolerance intervals use Bonferroni approximations where one sided intervals are calculated with adjusted α and p values as follows:
α = 0.5+0.5*(1-α) and p = (1+p)/2 for the lower interval
α = 0.5-0.5*(1-α) and p = (1-p)/2 for the upper interval
Nonparametric Intervals
One-Sided Lower Limit
The lower 100(1 - α)% one-sided tolerance limit to contain at least a proportion β of the sampled distribution from a sample of size n is the order statistic x(l). The index l is computed as follows:
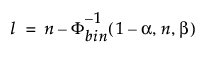
where Φ-1bin(1-α, n, β) is the (1 - α)th quantile of the binomial distribution with n trials and probability of success β.
The actual confidence level is computed as Φbin(n-l, n, β), where Φbin(x, n, β) is the probability of a binomially distributed random variable with n trials and probability of success β being less than or equal to x.
Note that to compute a lower one-sided distribution-free tolerance interval, the sample size n must be at least as large as 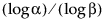 .
.
One-Sided Upper Limit
The upper 100(1 - α)% one-sided tolerance limit to contain at least a proportion β of the sampled distribution from a sample of size n is the order statistic x(u). The index u is computed as follows:
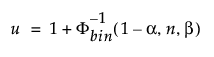
where Φ-1bin(1-α, n, β) is the (1 - α)th quantile of the binomial distribution with n trials and probability of success β.
The actual confidence level is computed as Φbin(u-1, n, β), where Φbin(x, n, β) is the probability of a binomially distributed random variable with n trials and probability of success β being less than or equal to x.
Note that to compute an upper one-sided distribution-free tolerance interval, the sample size n must be at least as large as 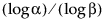 .
.
Two-Sided Interval
The 100(1 - α)% two-sided tolerance interval to contain at least a proportion β of the sampled distribution from a sample of size n is computed as follows:
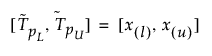
where x(i) is the ith order statistic and l and u are computed as follows:
Let ν = n - Φ-1bin(1-α, n, β), where Φ-1bin(1-α, n, β) is the (1 - α)th quantile of the binomial distribution with n trials and probability of success β. If ν is less than 2, a two-sided distribution-free tolerance interval cannot be computed. If ν is greater than or equal to 2, l = floor(ν/2) and u = floor(n + 1 - ν/2).
The actual confidence level is computed as Φbin(u-l-1, n, β), where Φbin(x, n, β) is the probability of a binomially distributed random variable with n trials and probability of success β being less than or equal to x.
Note that to compute a two-sided distribution-free tolerance interval, the sample size n must be at least as large as the n in the following equation:
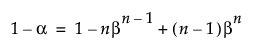
For more information about distribution-free tolerance intervals, see Meeker et al. (2017, sec. 5.3).