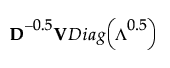Statistical Details for the Details Report
In the Multiple Correspondence Analysis platform, the details report lists singular values. The singular value decomposition used to obtain these values is an extension of the singular value decomposition used in a simple Correspondence Analysis.
When a simple Correspondence Analysis is performed, the report lists the singular values from the following singular value decomposition:
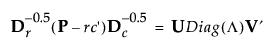
where:
• P is the matrix of counts divided by the total frequency.
• r and c are the row and column sums of P.
• The D matrices are diagonal matrices of the values of r and c.
• Λ is the column vector of singular values.
When Multiple Correspondence Analysis is performed, the singular value decomposition extends to the following equation:
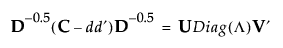
where:
• C is the Burt table.
• d is a column vector of the column sums of C (d is also the row sums, since C is symmetric).
• D is a diagonal matrix of the values of d.
In the Details report, the inertia is the column vector Λ. The singular value is the square root of the inertia vector. The column coordinates are calculated as follows: