多項式効果モデルの例
「モデルのあてはめ」プラットフォームの[標準最小2乗]手法を使って、二変量データに3次多項式をあてはめます。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Growth.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「比」を選択し、[Y]をクリックします。
4. 「次数」の横のテキストボックスに「3」と入力します。
5. 「月齢」を選択し、[マクロ]>[多項式の次数]を選択します。
モデルに3つの項が追加されます。
6. [実行]をクリックします。
表示される各レポートの内容を以下に説明していきます。
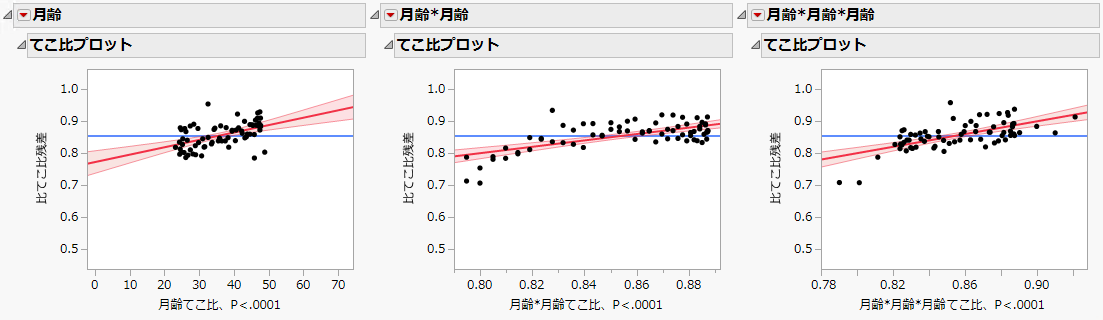
てこ比プロット
てこ比プロットは、現在の回帰モデルの結果に大きな影響を与えているデータ点を探し出すのに用います。
図4.2 てこ比プロット
てこ比プロットは、大きな影響を及ぼすデータ点がなく、モデルに使われているすべての説明変数が統計的に有意であることを示しています。
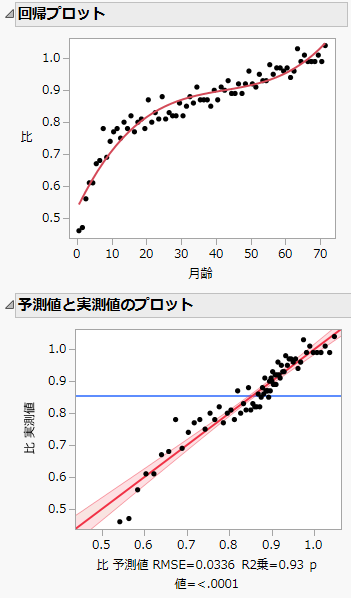
「回帰プロット」と「予測値と実測値のプロット」
「回帰プロット」と「予測値と実測値のプロット」を見ることで、モデルの予測性能や予測精度を評価できます。
図4.3 「回帰プロット」と「予測値と実測値のプロット」
「回帰プロット」には、データ点と3次多項式モデルが描かれています。「予測値と実測値のプロット」の点は、y = xの線に沿っており、モデルの予測値が実測値に近いことを示しています。
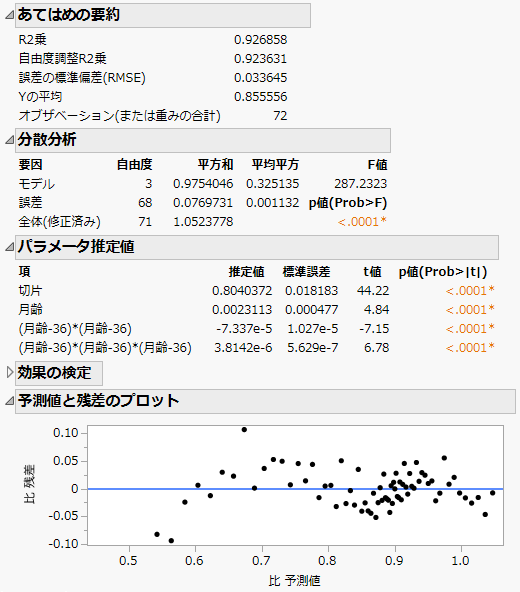
モデルの「あてはめの要約」表と残差プロット
「あてはめの要約」表では、モデルの適合度や応答変数の統計量を評価できます。「あてはめの要約」表には、モデルの適合度や応答変数の統計量が表示されています。「分散分析」表には、モデル全体の統計的な有意性や変動の要因が示されています。「パラメータ推定値」表には、回帰係数の点推定値・その標準誤差・そのp 値などが示されています。「効果の検定」表には、個々の説明変数に対するp値が示されています。「予測値と残差のプロット」表では、残差のパターンや傾向を確認することで、回帰モデルの仮定や性能を評価できます。
図4.4 回帰モデルの要約と残差分析
この例では、「分散分析」表でモデル全体は統計的に有意であることが示されています。また、「パラメータ推定値」表でモデルに含まれる説明変数のすべての係数が統計的に有意であることが示されています。また、「あてはめの要約」表ではR2乗値が0.927と大きくなっており、説明変数と応答変数の間に強い関係があることが示されています。
「予測値と残差のプロット」では、ゼロの線の上下対称に、ランダムに残差が散らばっています。このことは、モデルの仮定が満たされており、誤差が正規分布に従っているだろうことを示唆しています。