交互作用のある二元配置分散分析の例
「モデルのあてはめ」プラットフォームの[標準最小2乗]手法を使って、交互作用項のある二元配置分散分析を行います。ポップコーンの種類と一回にポップする量が、ポップコーンの収率に影響しているかを調べてみましょう。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Popcorn.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「収率」を選択し、[Y]をクリックします。
4. 「コーンの種類」、「一回にポップする量」を選択し、[マクロ]>[完全実施要因]を選択します。
5. [実行]をクリックします。
6. 「応答 収率」の赤い三角ボタンをクリックし、[因子プロファイル]>[プロファイル]を選択します。
表示される各レポートの内容を以下に説明していきます。
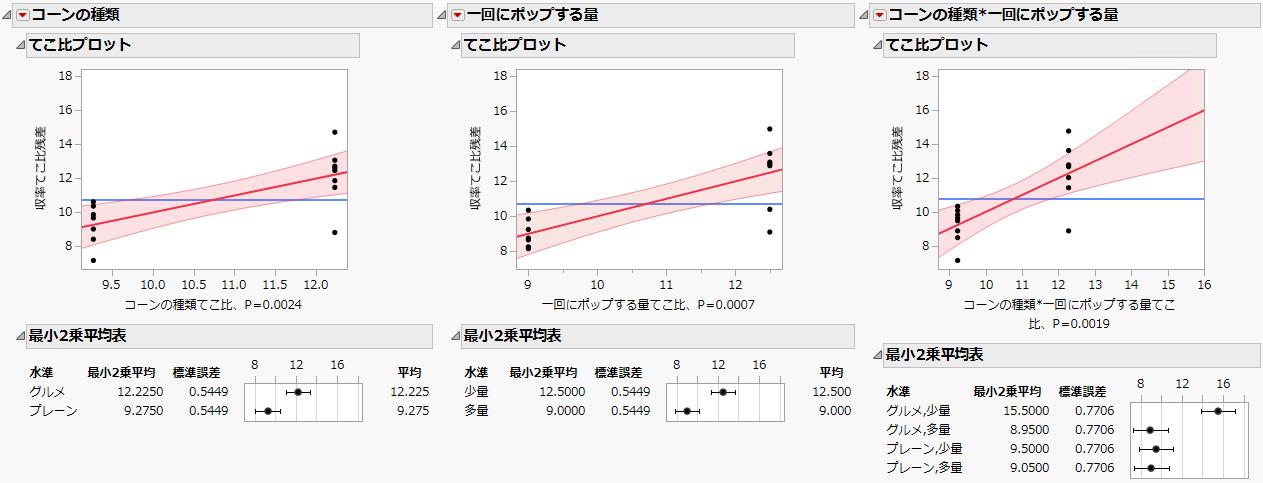
てこ比プロット
てこ比プロットは、現在の回帰モデルの結果に大きな影響を与えているデータ点を探し出すのに用います。
図4.12 因子とその交互作用の「てこ比プロット」と「最小2乗平均表」
「コーンの種類」および「一回にポップする量」の交互作用のてこ比プロットに描かれた予測値の線の傾きを見ると、これらの間に強い交互作用があると判断できます。
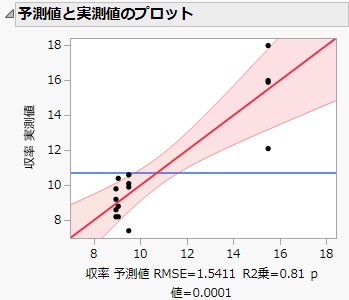
予測値と実測値のプロット
「予測値と実測値のプロット」では、「収率」の実測値と予測値を比較することで、モデルの予測性能や予測精度を評価できます。
図4.13 予測値と実測値のプロット
実測値と予測値の関係は、統計的に有意であると判断できます(p値=0.0001)。
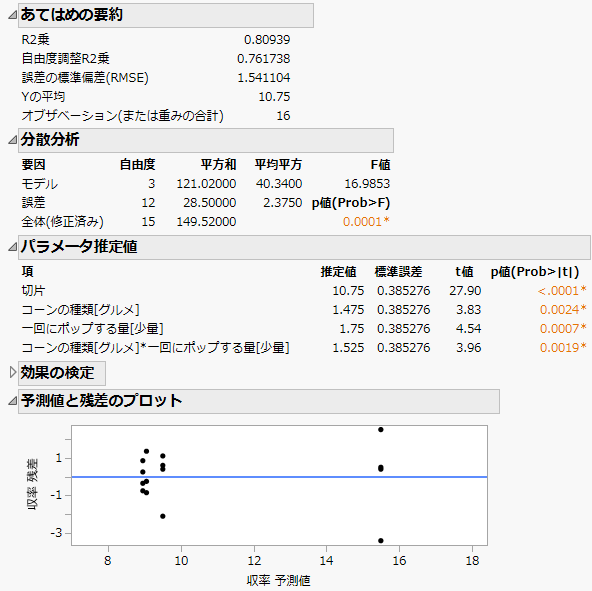
モデルの「あてはめの要約」表と残差プロット
「あてはめの要約」表では、モデルの適合度や応答変数の統計量を評価できます。「あてはめの要約」表には、モデルの適合度や応答変数の統計量が表示されています。「分散分析」表には、モデル全体の統計的な有意性や変動の要因が示されます。「パラメータ推定値」表には、回帰係数の点推定値・その標準誤差・そのp値などが示されています。「効果の検定」表には、個々の説明変数に対するp値が示されています。「予測値と残差のプロット」表では、残差のパターンや傾向を確認することで、回帰モデルの仮定や性能を評価できます。
図4.14 モデルの要約、分散分析、パラメータ、残差
回帰モデルのR2乗値が0.809であること、p値が0.0001であることは、推定されたモデルを予測に用いることの有用性を示しています。「回帰係数がゼロである」という帰無仮説に対する検定のp値も小さく、両方の因子およびその交互作用は統計的に有意です。
「予測値と残差のプロット」では、ゼロの線の上下対称に、ランダムに残差が散らばっています。このことは、モデルの仮定が満たされており、誤差が正規分布に従っているだろうことを示唆しています。
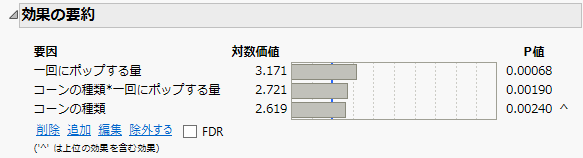
効果の要約
「効果の要約」表では、応答変数に対する各因子がもつ関連の強さや、統計的な有意性をすばやく評価できます。
図4.15 「効果の要約」表
3つの因子はすべて、対数価値が大きく、p値が非常に小さいことから、応答変数に対して統計的に有意な関連があることを示唆しています。
予測プロファイル
「予測プロファイル」では、因子の値に応じて応答の予測値がどのように変化するかを調べられます。
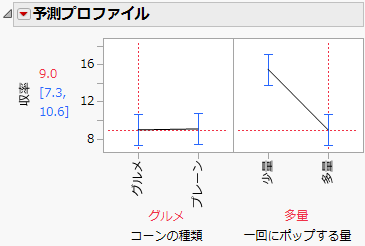
図4.16 予測プロファイル
グルメポップコーンの多量のバッチの場合、「収率」の予測値は9.0で、95%信頼区間は7.3~10.6です。予測プロファイルでは、「コーンの種類」および「一回にポップする量」の水準の組み合わせを変えたときに「収率」がどのように変化するかを対話的に調べることができます。予測プロファイルを用いたモデルの解釈の詳細については、二元配置分散分析の例を参照してください。