実験の損失を評価する例
「計画の評価」プラットフォームを使って、2つの実験が失われたときの影響を評価します。
テニスボールの反発係数に関する実験が行われ、3つの因子(シリカ・硫黄・シラン)の効果が調べられました。実験の目的は、「反発係数」を予測するモデルを作成することです。「応答曲面計画」プラットフォームを使い、実験回数15のBox-Behnken計画を選択しました。研究者は、実験終了後、「シリカ」 = 0.7と「シラン」 = 50を用いた2つの実験において、これらが正しく処理されていなかったことに気が付きました。これらの実験をデータの分析に含めることはできません。
この例では、意図していた計画として「Bounce Data.jmp」の計画を使用します。そして、その計画から2つの実験を除外した計画を、実際に実施する計画とします。「計画の評価」プラットフォームを使って、予定していた実験から2つの実験が失われたときの影響を評価します。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Design Experiment」フォルダの「Bounce Data.jmp」を開きます。
以下の手順で、実験回数15のうち、「シリカ」の値が0.7、「シラン」の値が50である2つの実験を除外します。データテーブルでは、行3と行7に当たります。
2. 行3と行7を選択し、強調表示部分を右クリックして[行]>[行の選択]>[選択行の逆転]を選択します。
3. [テーブル]>[サブセット]を選択して[OK]をクリックします。
4. [実験計画(DOE)]>[計画の診断]>[計画の比較]を選択します。
5. 「「Bouce Dataのサブセット」と比較する計画」として、「Bounce Data」を選択します。
6. 「元の列」として、両方の計画で「シリカ」・「硫黄」・「シラン」を選択します。
7. [OK]をクリックします。
これで、2つの計画の比較が可能になります。
検出力分析
検出力分析を行うために、次のステップを実行します。
8. 「RMSEの予想値」に「2」と入力します。また、デフォルトでは、誤差の標準偏差(「RMSEの予想値」)は1と仮定されています。ここでは、過去に行った調査から、RMSEはおよそ2であることがわかっているものとします。
9. ここでは、交互作用項や2乗項は応答に影響していないものとして、「因子を最小から最大に変更したときに応答平均が6単位だけ変化する差」差を検出できるかどうかを調べます。「係数の予想値」を全項で「3」に設定します。
10. [係数の予想値に基づき変更]をクリックします。
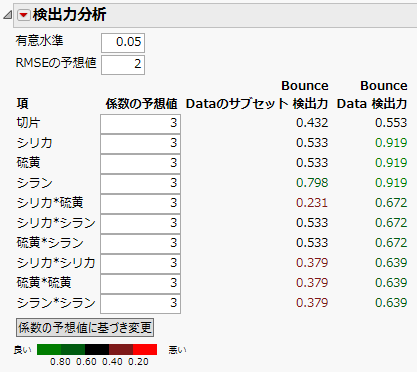
図17.30 検出力分析
実際の計画における検出力は、意図した計画のものより一様に小さくなっています。「シリカ」と「硫黄」の主効果に関しては、意図した計画における検出力は、実際の計画のおよそ2倍です。ちなみに、「シリカ」と「硫黄」の交互作用を見ると、検定の検出力は、実際の計画で0.231、意図した計画では0.672になっています。このように、実際の計画は意図した計画に比べて検出力が大幅に低下しています。
予測分散プロファイル
そして、下方向にスクロールして「予測分散プロファイル」を表示します。
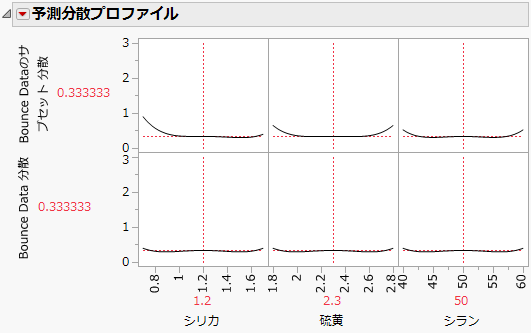
図17.31 実際の計画(上)と意図した計画(下)の予測分散プロファイル
「予測分散プロファイル」プロットは、相対的な予測分散をプロットしたものです。計画領域のさまざまな位置における相対的な予測分散を調べることができます。
計画領域の中央を見ると、相対的な予測分散はどちらのプロットでも同じです。しかし、計画領域の端の方を見ると、分散は意図した計画より実際の計画の方が大きいようです。
11. 「予測分散プロファイル」の赤い三角ボタンをクリックし、[予測分散の最大化]を選択します。
どちらの計画も、「シリカ」=0.7、「硫黄」=1.8、「シラン」=40の計画点で予測分散が最大になっています。意図した計画では、予測分散の最大値は1.396でした。しかし実験の少ない実際の計画では、予測分散の最大値は3.021にもなります。予測分散が最大になる設定の組み合わせは他にもあることに注意してください。実際の計画の方が最大予測分散が大きいのは、計画領域の一部における予測の精度が、意図した通りに計画を実施した場合より低いことを意味します。
計画領域率プロット
スクロールして「計画領域率プロット」に移動します。
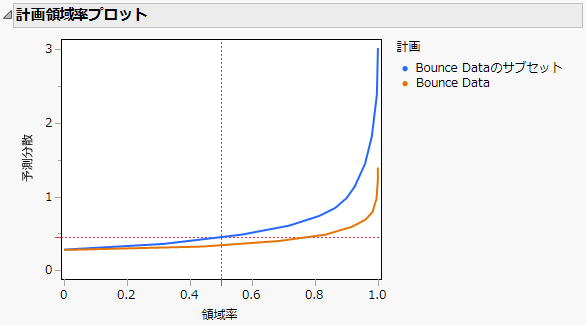
図17.32 計画領域率プロット
実際の計画の相対的な予測分散は、計画領域全体で、意図した計画のそれより大きいことがわかります。その差は、領域が広くなるにつれて大きくなっています。
推定効率
スクロールして「相対推定効率」に移動します。
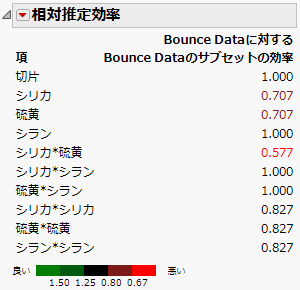
図17.33 相対推定効率
「シリカ」または「硫黄」を含む効果の相対推定効率は、実際の計画の方が意図した計画より低くなっています。
相関のカラーマップ
スクロールして「相関のカラーマップ」に移動し、カラーマップを開きます。
図17.34 意図した計画(左)と実際の計画(右)の相関のカラーマップ
2つのカラーマップに、「モデル」の効果が表示されます。どちらのプロットも、効果間における相関係数の絶対値を、その大きさに応じて、白~黒のスケールで示しています。効果の間に相関がまったく無いか、ごく小さな相関しかない状況が理想です。相関係数の絶対値は、実際の計画におけるカラーマップを見ると、意図した計画のそれより大きくなっています。たとえば、「硫黄」と「シリカ*硫黄」間の相関は、意図した計画では0.0001より小さいですが、実際の計画では0.5774になっています。
計画の診断統計量
スクロールして「計画の診断統計量」セクションに移動します。
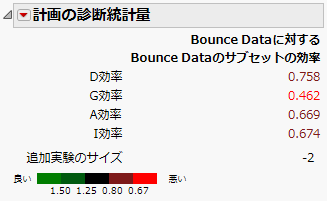
図17.35 計画の診断統計量
意図した計画の効率は、実際の計画より低いことがわかります。これらの結果から、2つの実験を除外することは、悪い影響を与えることが分かります。
計画の効率は、実験回数とモデル行列の両方によって決まります。ある計画のD-効率・G-効率・A-効率は、同じ実験回数での理想的な計画と比較して求められます。実験回数が多い計画のほうが、少ない計画に比べて常にこれらの指標が大きくなるわけではありません。効率の定義については、計画の診断統計量を参照してください。