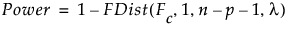1つのパラメータに対する検出力
この節では、1つの計画パラメータに対する検定の検出力について説明します。次のような表記を使用します。
X
計画行列（デザイン行列）。名義尺度効果のコード変換については、『基本的な回帰モデル』の「Statistical Details for Nominal Effects Coding」を参照してください。また、モデル行列も参照してください。
メモ: 計画行列を表示するには、［モデルのあてはめ］を実行します。その後、レポートの赤い三角ボタンのメニューから［列の保存］>［コーディングのテーブルを保存］を選択します。
bi
調べたい項に対応するパラメータ。
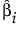
最小2乗法で求めたbiの推定値。
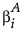
「係数の予想値」の値。2水準の名義変数である場合、それら2水準の応答平均の差は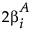
となります。
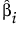の分散は、
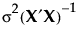のi番目の対角要素で与えられます。ここで、σ2は誤差分散です。
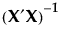のi番目の対角要素を
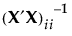とします。
誤差分散のσ2は、平均2乗誤差（MSE; Mean Squared Error）によって推定され、その自由度はn − p − 1です。ここで、nは標本サイズ、pは切片を除くモデル項の数です。n − p − 1 = 0の場合、誤差の自由度は1に設定されます。自由度を0に設定することにより、飽和計画でもパラメータに対する検出力を算出します。
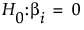の検定に対する検定統計量であるF値は、次のようになります。
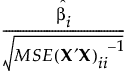
これは次のような式による検定と等価です。
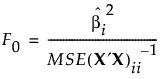
帰無仮説の下では、検定統計量F0は、分子自由度が1で、分母自由度がn − p − 1のF分布に従います。
もし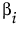
の真値が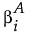
である場合、F0は次のような式で求められる非心パラメータを持つ非心F分布に従います。
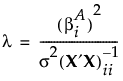
検定の検出力を求めるには、まず、有意水準がaである棄却値Fcを求めます。
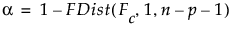
そして、次式で検出力を計算します。
