「多重因子分析」プラットフォームのオプション
「多重因子分析」の赤い三角ボタンのメニューには、以下のオプションが含まれています。
ブロックに対する重み
ブロックごとに計算された第1固有値、および、コンセンサス主成分分析を行うときに使われる各ブロックへの重みの表示/非表示を切り替えます。「重み」は、第1固有値の平方根の逆数です。
固有値
固有値表の表示/非表示を切り替えます。この表には、コンセンサスの次元に対応する固有値が降順に表示されます。
固有ベクトル
固有ベクトル表の表示/非表示を切り替えます。この表には、コンセンサスの各次元に対する固有ベクトルが表示されます。左から順に、第1次元目、第2次元目、…と表示されます。これらの固有ベクトルを使って元の変数から線形結合を計算したものが、コンセンサス主成分分析における主成分スコアです。
変数の負荷量
コンセンサス主成分分析から計算された主成分負荷量の表示/非表示を切り替えます。主成分分析と同様に、負荷量は変数と成分の相関を表します。ゼロに近い値は、コンセンサスの次元に対する影響がほとんどないことを意味します。
変数の偏寄与率
変数の偏寄与率(partial contribution of a variable)の表示/非表示を切り替えます。この値は、コンセンサスの次元に対して各変数がどの程度寄与しているかを、分散の割合でパーセントを単位として示したもの(該当の次元における分散のうち、各変数がどれだけ説明しているかを表した寄与率)です。
変数の余弦2乗
「変数の余弦2乗」(squared cosine of a variable)の表示/非表示を切り替えます。変数ごとに、この余弦2乗をすべての次元について足し合わせると、1(100%)になります。この余弦2乗は、変数と次元間の重なりを分散で表しています。
ヒント: 変数の偏寄与率が0に近いほど、該当の次元はその変数では構成されていないことを意味しています。また、変数の余弦2乗が0に近いほど、該当の次元はその変数を説明していないことを意味しています。表に示されている数値の濃淡は、それらの大きさを表しています。
要約プロット
要約プロットの表示/非表示を切り替えます。要約プロットには、固有値プロット、スコアプロット、負荷量プロットが含まれます。
コンセンサスマップ
コンセンサスマップの表示/非表示を切り替えます。コンセンサスマップを参照してください。
バイプロット
スコアプロットと負荷量プロットを重ねたプロットの表示/非表示を切り替えます。コントロールを使用してプロットの2つの次元を選択できます。
部分主成分軸プロット
部分主成分軸プロット(partial axis plot)の表示/非表示を切り替えます。このグラフは、ブロックごとの主成分分析における主成分スコアと、コンセンサス主成分分析における主成分スコアとの相関係数をプロットしたものです。コントロールを使用してプロットの2つの次元を選択できます。凡例のブロックをクリックすると、該当するブロックがプロットで強調表示されます。
表示オプション
矢印線
負荷量プロットと部分主成分軸プロットの矢印の表示/非表示を切り替えます。矢印は、変数の総数が1000以下のときに表示されます。変数の総数が1000を超える場合は、矢印はデフォルトでは表示されません。
ラベルの表示
コンセンサスマップやバイプロットでは、すべての点におけるブロック名ラベルの表示/非表示を切り替えます。部分主成分軸プロットでは、すべての点における列名ラベルの表示/非表示を切り替えます。
ヒント: コンセンサスマップの重心や負荷量プロットのデータ点を識別するには、行ラベルを使用してください。
ブロックの偏寄与率
「ブロックの偏寄与率」の表示/非表示を切り替えます。これは、ブロックが該当の次元にどれぐらい寄与しているかを示す寄与率です。ブロック内に含まれている変数の偏寄与率を合計したものです。
ブロックの偏慣性
尺度を変更したブロックの偏寄与率の表示/非表示を切り替えます。これは、「ブロックの偏寄与率」にコンセンサス主成分分析の固有値を掛け合わせ、100で割った値です。
ブロックの余弦2乗
「ブロックの余弦2乗」の表示/非表示を切り替えます。これは、ブロックごとに「ブロックの偏慣性」を2乗して、固有値を計算するのに用いた平方和で割ったものです。値の範囲は0~1です。この値は、ブロックの分散のうち各主成分によって説明される割合です。
ブロック偏スコアと全体との相関
ブロックごとに求められた偏主成分スコアと、コンセンサス主成分の主成分スコアとの相関係数を要素とする行列の表示/非表示を切り替えます。同じ次元どうしの相関係数のみが表示されるため、行列は長方形になります。
RV相関
RV相関を要素とする行列の表示/非表示を切り替えます。RV相関は、ブロック間における関係の大きさを、相関係数の2乗のようなもので表した指標です。
Lg係数
Lg係数を要素とする行列の表示/非表示を切り替えます。Lg係数は、ブロック間の関係の大きさを、共分散の2乗のようなもので表した指標です。
データ行のスコアを保存
コンセンサス主成分分析から計算される主成分スコアを、データテーブルの新しい列に保存します。カテゴリカルな追加変数を1つまたは複数使用した場合は、それらの変数の水準ごとの主成分スコアも新しいデータテーブルに保存されます。
データ行の余弦2乗を保存
各データ行の余弦2乗を、データテーブルの新しい列に保存します。カテゴリカルな追加変数を1つまたは複数使用した場合は、その余弦2乗も新しいデータテーブルに保存されます。
データ行の偏寄与率を保存
各データ行の偏寄与率を、データテーブルの新しい列に保存します。カテゴリカルな追加変数を1つまたは複数使用した場合は、その偏寄与率も新しいデータテーブルに保存されます。
ブロックの偏スコアを保存
ブロックの偏スコアを新しいデータテーブルに保存します。
部分主成分軸の座標を保存
部分主成分軸の座標を新しいデータテーブルに保存します。
以下のオプションの詳細については、『JMPの使用法』の「JMPレポートのローカルデータフィルタ」、「JMPレポートの[やり直し]メニュー」、および「JMPレポートの[スクリプトの保存]メニュー」を参照してください。
ローカルデータフィルタ
データをフィルタリングするためのローカルデータフィルタの表示/非表示を切り替えます。
やり直し
分析を繰り返したり、やり直したりするオプションを含みます。また、[自動再計算]オプションに対応しているプラットフォームにおいては、[自動再計算]オプションを選択すると、データテーブルに加えた変更が、該当するレポートに即座に反映されるようになります。
プラットフォーム環境設定
現在のプラットフォームの環境設定を表示したり、現在のJMPレポートの設定に合わせて環境設定を変更したりできます。
スクリプトの保存
レポートを再現するためのスクリプトを保存するオプションが、保存先ごとに用意されています。
メモ: このプラットフォームには、他にもスクリプトだけで使用できるオプションがあります。[ヘルプ]メニューの[スクリプトの索引]を開いてください。また、[スクリプトの索引]には、この節で紹介されているオプションのスクリプト例もあります。
「多重因子分析」プラットフォームの統計的詳細
多重因子分析では、複数の部分テーブル(sub-tables)から、互いに直交する主成分スコアを求めます。基本的な手順は以下のとおりです。
• それぞれの部分テーブルに対する主成分分析を個別に行います。
• それぞれの部分テーブルの第1固有値から、重みを算出します。
• 部分テーブルを左右に連結し、まず、各列を平均0分散1に標準化します。
• 標準化した行列に対して、部分テーブルごとに重みを掛け合わせます。その重みを掛け合わされた行列に対して特異値分解を行います。これは、部分テーブルごとの重みを考慮した一般化特異値分解を標準化した行列に対して行うのと等価です。この計算を、「コンセンサス主成分分析」と言います。つまり、部分テーブルに対して重みを与えたものに主成分分析を適用します。
上記の手順によって、右特異ベクトル、左特異ベクトル、特異値という3つの行列が求められます。これらの行列から、コンセンサス主成分分析の主成分スコア、固有値、主成分負荷量が求められます。これらの3つの行列は、元のデータに含まれるさまざまな列を少数の次元にまで縮小したものになっています。最初の数次元を調べることにより、商品の類似度や相違性を判断することができます。
計算
多重因子分析における行列Xの特異値分解は、以下のように定義することができます。
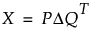 ここで、
ここで、 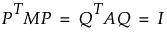
各行列の定義は以下のとおりです。
Xは、部分テーブルから成るn × pの行列で、平均0分散1に標準化されています。官能検査のデータでは、n個の商品(製品、食品)と、複数の評価者から得られたp種類の評価に該当します。
Qは、右特異ベクトルから成るp × qの行列です。q個の主成分負荷量を計算するのに使用されます。
Dは、特異値から成るq × qの対角行列です。主成分分析と同様に、特異値の2乗は固有値であり、各主成分の重要度を表しています。
Pは、左特異ベクトルから成るn × qの行列です。q個の主成分スコアを求めるのに使用されます。
Mは、各データ行の重み(度数)を示すn × nの対角行列です。
Aは、ブロックの重みから成る、p × pの対角行列です。
多重因子分析の詳細については、Abdi et al.(2013)を参照してください。
慣性の計算について
JMPでは、慣性(分散)を計算する際にN - 1を使用しています。これらの計算は、データ行とブロックに対するスコアの計算に影響します。