D-최적과 I-최적의 반응 표면 설계 비교
사용자 설계 플랫폼 및 설계 비교 플랫폼을 사용하여 2요인 반응 표면 설계 컨텍스트에서 I-최적과 D-최적 간의 차이를 탐색합니다.
I-최적 설계
1. DOE > 사용자 설계를 선택합니다.
2. N개 요인 추가 옆에 2를 입력합니다.
3. 요인 추가 > 연속형을 클릭합니다.
4. 계속을 클릭합니다.
5. RSM을 클릭합니다.
X1과 X2의 2차 및 교호작용 항이 모형에 추가됩니다. RSM 항을 추가했으므로 "권장 사항" 최적 기준이 "D-최적"에서 "I-최적"으로 변경됩니다. 나중에 "설계 진단" 섹션에서 이를 확인할 수 있습니다.
참고: 다음 두 단계에서 난수 시드값을 설정하면 이 예에 표시된 결과가 재현됩니다. 설계를 직접 구성할 때는 이러한 단계가 필요하지 않습니다.
6. (선택 사항) "사용자 설계"의 빨간색 삼각형을 클릭하고 난수 시드값 설정을 선택한 후 123를 입력하고 확인을 클릭합니다.
7. (선택 사항) "사용자 설계"의 빨간색 삼각형을 클릭하고 시작 수를 선택한 후 5를 입력하고 확인을 클릭합니다.
8. 설계 생성을 클릭합니다.
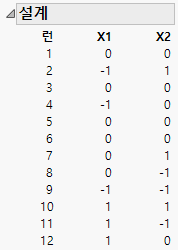
그림 5.38 I-최적 설계
이 I-최적 설계에서 런 1, 3, 5, 6은 중앙점(X1 = 0, X2 = 0)에 있습니다. I-최적 설계는 D-최적 설계와 비교하여 설계 공간의 중심에 더 많은 런을 배치하는 경향이 있습니다. 따라서 극단에 배치되는 런의 수가 더 적습니다.
9. 테이블 생성을 클릭한 후 IOptDesign으로 저장합니다.
이 데이터 테이블에는 I-최적 설계가 포함됩니다. 이 테이블을 열어 두십시오. 다음 섹션에서 D-최적 설계를 생성하고 두 설계를 비교해 보겠습니다.
D-최적 설계
I-최적 설계 및 D-최적 설계에 대한 예측 분산 프로파일과 설계 공간 비율 그림을 비교하려면 다음을 수행하십시오.
1. I-최적 설계를 포함하는 "사용자 설계" 창에서 뒤로를 클릭합니다.
참고: 다음 두 단계에서 난수 시드값과 시작 수를 설정하면 이 예에 표시된 결과가 재현됩니다. 설계를 직접 구성할 때는 이러한 단계가 필요하지 않습니다.
2. (선택 사항) "사용자 설계"의 빨간색 삼각형을 클릭하고 난수 시드값 설정을 선택한 후 123를 입력하고 확인을 클릭합니다.
3. (선택 사항) "사용자 설계"의 빨간색 삼각형을 클릭하고 시작 수를 선택한 후 5를 입력하고 확인을 클릭합니다.
4. "사용자 설계"의 빨간색 삼각형을 클릭하고 최적 기준 > D-최적 설계 생성을 선택합니다.
5. 설계 생성을 클릭합니다.
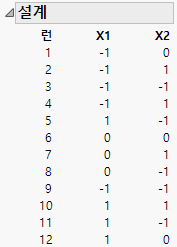
그림 5.39 D-최적 설계
이 D-최적 설계에서는 런 6만 중앙점에 있습니다. D-최적 설계는 I-최적 설계와 비교하여 설계 공간의 극단에 더 많은 런을 배치하는 경향이 있습니다. I-최적 설계의 중앙점 런은 4개였습니다.
6. 테이블 생성을 클릭한 후 DOptDesign으로 저장합니다.
설계 비교
1. IOptDesign 테이블을 클릭하여 활성화합니다.
2. DOE > 설계 진단 > 설계 비교를 선택합니다.
3. IOptDesgin과 비교할 DOptDesign을 선택하고 "확인"을 클릭합니다.
4. 예측 분산 프로파일로 스크롤합니다.
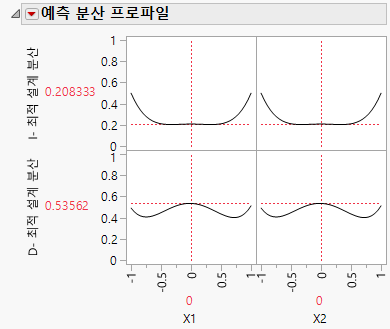
그림 5.40 예측 분산 프로파일 비교
설계 영역의 중심에서 상대 예측 분산은 0.53562이며, I-최적 설계의 경우 0.208333이었습니다. 이는 상대 표준 오차가 D-최적 설계의 경우 0.732이고 I-최적 설계의 경우 0.456이라는 의미입니다. 다른 조건이 모두 같다고 가정할 때 설계 영역의 중심에서 D-최적 설계의 기대 반응에 대한 신뢰 구간이 I-최적 설계의 경우보다 약 60% 더 넓습니다.
"설계" 섹션에서는 D-최적 설계에 -1, 0, 1로 설정된 X1과 X2의 모든 조합에 대해 하나씩, 총 9개의 설계점이 있음을 보여 줍니다. D-최적 기준은 이러한 각 설계점에서 상대 예측 분산을 낮추려고 합니다. X1 및 X2의 슬라이더를 -1과 1로 움직여 설계 영역의 극단에서 분산을 탐색합니다. 이러한 극점에서의 분산은 대개 같은 지점에서 I-최적 설계의 분산보다 작습니다.
5. 설계 공간 비율 그림으로 스크롤합니다.
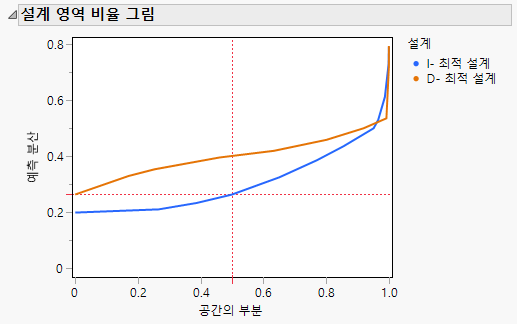
그림 5.41 설계 공간 비율 그림
각 그림의 빨간색 십자기호는 설계 공간의 50%에 대한 최대 예측 분산을 나타냅니다. 설계 공간의 50%에 대한 I-최적 설계의 예측 분산은 약 0.27 미만입니다. D-최적 설계의 경우 예측 분산은 약 0.4입니다.
I-최적 설계의 분산 곡선은 설계 공간의 90% 이상에서 D-최적 설계의 분산 곡선 아래에 있습니다. 이는 I-최적 기준이 전체 설계 공간에서 예측 분산을 최소화하려고 한다는 사실을 반영합니다. 반면에 D-최적 기준은 모형 항을 더 잘 추정하는 데 중점을 둡니다.