잠재 성장 곡선 모형의 예
LGC(잠재 성장 곡선) 모형을 사용하면 분석자가 종단 데이터를 모델링하고 시간에 따른 궤적을 특성화할 수 있습니다. 가장 일반적인 잠재 성장 곡선 모형은 과정의 전체 궤적과 전체 궤적에서 개별 관측값의 편차를 포착하기 위해 절편 및 기울기 잠재 변수를 지정하는 선형 성장 모형입니다. 이 모형은 랜덤 계수 모형과 매우 유사합니다. LGC 모형의 주요 특징은 데이터의 평균 구조에 제약 조건을 적용하는 것입니다. 평균 구조를 모델링하면 성장과 관련된 가설을 검정할 수 있습니다.
이 예에서는 선다형 시험 스코어를 사용하여 4년 동안 학업 프로그램을 이수한 학생들의 성취도를 모델링합니다. 선형 궤적이 이 과정의 특징이라는 가설을 검정하려고 합니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Academic Achievement.jmp를 엽니다.
2. 분석 > 다변량 방법 > 구조 방정식 모형을 선택합니다.
3. Multiple Choice Year1 ~ Multiple Choice Year4를 선택하고 모형 변수를 클릭합니다.
4. 확인을 클릭합니다.
"구조 방정식 모형" 보고서의 "모형 규격" 개요가 나타납니다.
5. 모형 바로 가기 > 종단 분석 > 선형 잠재 성장 곡선을 선택합니다.
이제 모형 규격 다이어그램에 선형 잠재 성장 곡선 모형이 표시됩니다.
6. 보기 패널 상자에서 목록 탭을 클릭합니다.
7. "분산" 목록에서 처음 4개 항목을 선택하고 등가 설정을 클릭합니다.
이렇게 하면 각 변수의 잔차 분산이 동일한 값으로 제한되며 이는 분산 가정의 동질성과 유사합니다. SEM에서는 이 가정을 검정할 수 있으므로 등식 제약 조건 없이 다른 모형을 적합시키고 카이제곱 차이 검정과 비교할 수 있습니다.
8. "모형 이름" 아래의 텍스트 상자에 "Linear LGC with Equal Variances"를 입력합니다.
9. 실행을 클릭합니다.
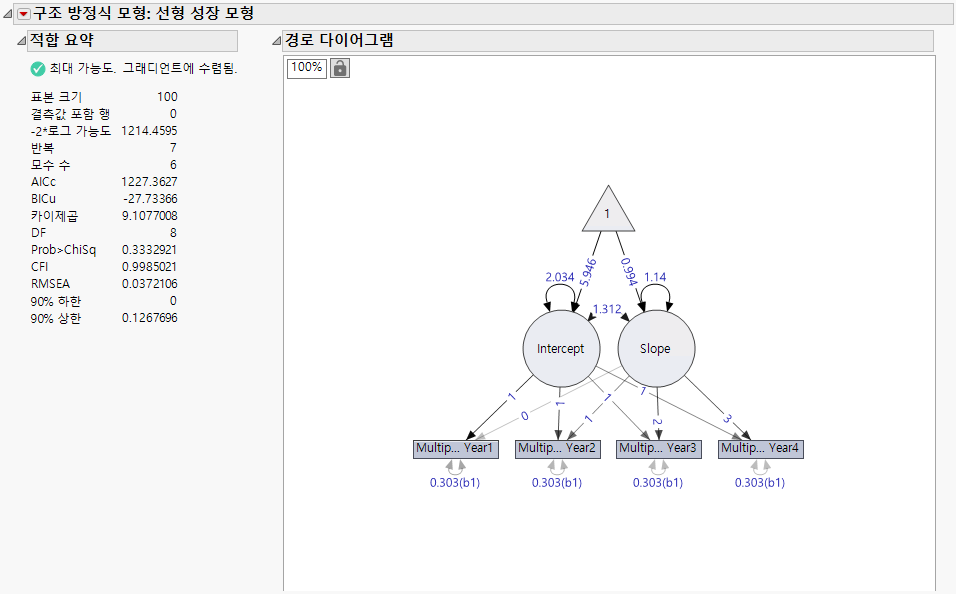
그림 8.11 선형 LGC 모형에 대한 적합 요약 및 경로 다이어그램
"적합 요약" 보고서에 나열된 이 모형의 카이제곱 통계량은 4.18이고 자유도는 8입니다. 해당 p 값은 0.3739로, 유의하지 않습니다. 이는 모형이 잘 적합된다는 귀무가설을 기각할 증거가 없음을 나타냅니다. 따라서 이 모형이 데이터를 적절하게 적합시킨다는 결론을 내릴 수 있습니다. 또한 CFI 및 RMSEA 적합 지수가 각각 0.9보다 크고 0.1보다 작으므로 적합도가 우수하다는 것을 나타냅니다.
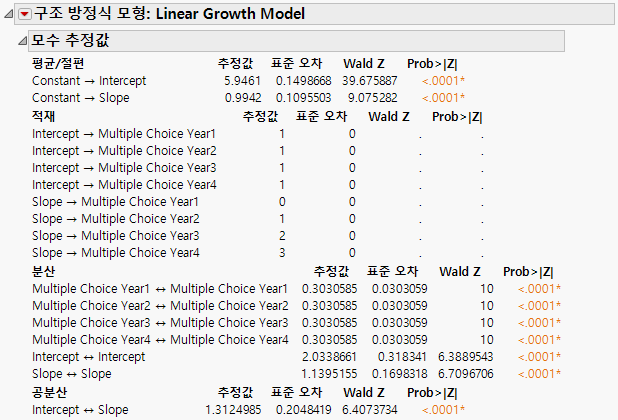
그림 8.12 선형 LGC 모형에 대한 모수 추정값
절편의 평균 추정값은 5.96이며, 이는 첫 해의 전체 성취도를 나타냅니다. 즉, 첫 번째 측정에서 학생들의 학업 성취도가 평균 5.96입니다. 첫 번째 측정에 해당하는 변수에 대한 기울기 요인의 적재가 0이므로 절편의 평균은 이 변수에서 중심화됩니다.
기울기의 평균 추정값은 0.95이며, 이는 전체 성취도가 매년 0.95씩 증가한다는 것을 나타냅니다. 절편 및 기울기 요인의 분산 추정값이 유의하므로 평균 궤적의 유의한 변동을 나타냅니다. 학생들마다 시작 지점도 다르고 증가 비율도 다릅니다. 외부 변수를 절편 및 기울기의 예측 변수로 사용하여 개인의 궤적 차이를 발생시키는 요인을 파악할 수 있습니다.
마지막으로, 절편과 기울기 사이의 양의 공분산은 첫 해에 더 높은 수준의 학업 성취도로 시작하는 학생이 시간이 지남에 따라 더 빠르게 증가하는 경향이 있음을 나타냅니다.
LGC 모형은 시간에 따른 과정 변화를 조사하기 위한 유연한 접근 방식을 제공합니다. "모형 바로 가기" 메뉴는 무성장 궤적, 2차 궤적 및 잠재 변수 기반 비선형 궤적을 포함하여 최량 모형 적합을 확인하기 위해 서로 적합시키고 검정할 수 있는 대안 궤적을 제공합니다.