다항식 효과 모형의 예
모형 적합 플랫폼의 표준 최소 제곱 분석법을 사용하여 3차 다항식 모형을 이변량 데이터에 적합시킵니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Growth.jmp를 엽니다.
2. 분석 > 모형 적합을 선택합니다.
3. ratio를 선택하고 Y를 클릭합니다.
4. 차수 옆의 텍스트 상자에 "3"을 입력합니다.
5. age를 선택하고 매크로 > 특정 차수까지의 다항식을 클릭합니다.
세 개의 항이 모형에 추가됩니다.
6. 실행을 클릭합니다.
아래에 보고서 섹션이 표시되고 설명이 나옵니다.
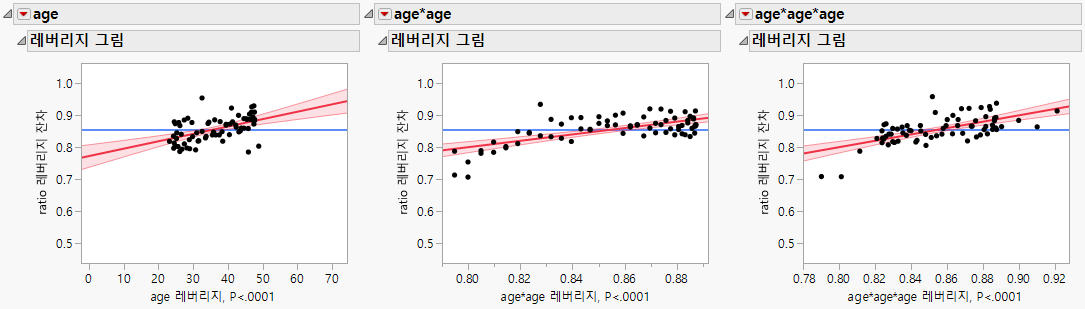
레버리지 그림
레버리지 그림을 사용하여 영향력 있는 관측값을 식별하고 회귀 모형에 미치는 영향을 평가할 수 있습니다.
그림 4.2 레버리지 그림
레버리지 그림에 영향력 있는 데이터 점이 표시되지 않고 모형의 모든 변수가 유의한 것으로 나타납니다.
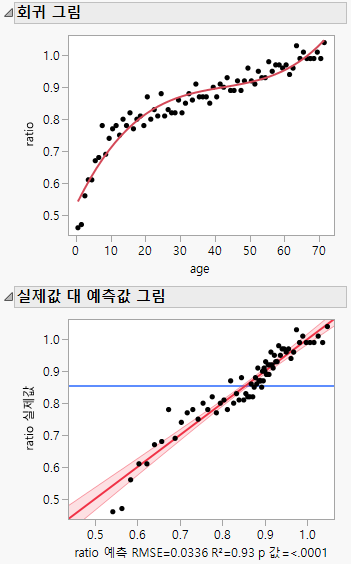
회귀 그림 및 실제값 대 예측값 그림
회귀 그림 및 실제값 대 예측값 그림을 사용하여 모형의 성능과 정확성을 평가할 수 있습니다.
그림 4.3 회귀 그림 및 실제값 대 예측값 그림
"회귀 그림"에는 데이터 점과 해당 데이터에 대한 비선형(3차 다항식) 회귀 모형 적합이 표시됩니다. "실제값 대 예측값 그림"의 점은 y = x 선을 따르며, 이는 모형 예측이 실제값에 가깝다는 것을 나타냅니다.
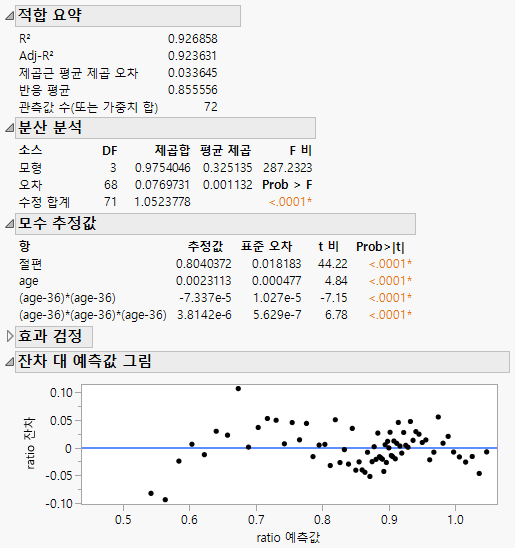
모형 적합 요약 테이블 및 잔차 그림
보고서의 테이블을 사용하여 모형 적합 및 반응 변수 통계량을 평가할 수 있습니다. "적합 요약" 테이블에는 모형 적합 및 반응 변수 통계량을 평가하기 위한 정보가 포함됩니다. "분산 분석" 테이블에는 전체 모형 유의성 및 변동 소스에 대한 정보가 포함됩니다. "모수 추정값" 테이블에는 계수, 표준 오차 및 예측 변수 유의성이 포함됩니다. "효과 검정" 테이블에는 개별 예측 변수의 유의성에 대한 정보가 포함됩니다. "잔차 대 예측값 그림"은 예측값 범위에서 잔차의 패턴 또는 추세를 검토하여 회귀 모형의 가정과 성능을 평가하는 데 사용됩니다.
그림 4.4 회귀 모형 요약 및 잔차 분석
이 예에서 "분산 분석" 테이블과 "모수 추정값" 테이블은 모형이 통계적으로 유의하고, 모형에 포함된 변수의 모든 계수가 각각 통계적으로 유의하다는 것을 나타냅니다. 또한 "적합 요약" 테이블에 표시된 높은 R² 값(0.927)은 예측 변수와 반응 변수 사이의 강한 관계를 나타냅니다.
"잔차 대 예측값 그림"은 잔차가 0 선 위와 아래에 무작위로 흩어져 있고 균등하게 분포되어 있음을 보여 줍니다. 이는 모형 가정이 충족되고 잔차가 정규 분포를 따른다는 의미입니다.