단순 생존 분포 적합의 예
이 섹션에는 비선형 플랫폼에서 단순 생존 분포를 적합시키는 예가 포함되어 있습니다.
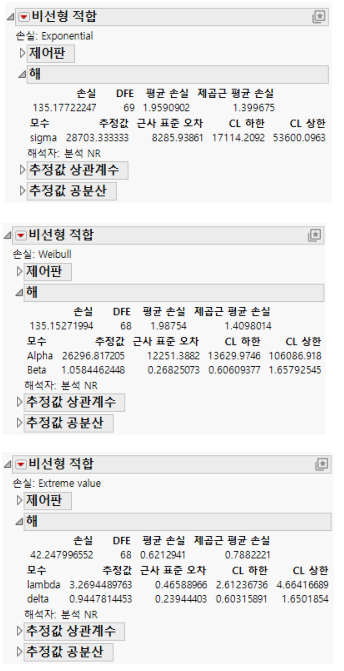
지수, Weibull 및 극단값 손실 함수
비선형 플랫폼을 사용하여 지수, Weibull 및 극단값 손실 함수를 고장 시간 데이터에 적합시킬 수 있습니다. 이 예의 데이터는 총 30만 시간의 서비스 시간이 누적된 70개 디젤 팬을 대상으로 한 연구에서 가져왔습니다. 팬은 서로 다른 여러 시간에 서비스되었습니다. 반응은 팬의 고장 시간 또는 중도절단 시 실행 시간입니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Reliability/Fan.jmp를 엽니다.
팁: 손실 함수에 대한 계산식을 보려면 Fan.jmp 데이터 테이블에서 Exponential, Weibull 및 Extreme value 열을 마우스 오른쪽 버튼으로 클릭하고 계산식을 선택합니다.
2. 분석 > 전문 모델링 > 비선형을 선택합니다.
3. Exponential을 선택하고 손실을 클릭합니다.
4. 확인을 클릭합니다.
5. 손실이 음의 로그 가능도임 체크박스가 선택되어 있는지 확인합니다.
6. 시작을 클릭합니다.
7. 신뢰 한계를 클릭합니다.
8. Exponential 대신 Weibull과 Extreme value를 선택하여 이 단계를 반복합니다.
그림 15.28 비선형 적합 결과
로그 정규 손실 함수
로그 정규 분포는 데이터 범위가 e의 여러 거듭제곱인 경우에 유용합니다. 로그 정규 손실 함수는 모수의 시작 값에 매우 민감할 수 있습니다. 로그 정규 분포는 정규 분포와 비슷하므로 Time의 자연 로그인 새 변수를 생성하고 분포를 사용하여 이 열의 평균 및 표준편차를 찾을 수 있습니다. 그런 다음 해당 값을 비선형 플랫폼의 시작 값으로 사용합니다. 이 예에서는 Time의 자연 로그 평균이 4.72이고 표준편차가 0.35입니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Reliability/Locomotive.jmp를 엽니다.
팁: 손실 함수에 대한 계산식을 보려면 Locomotive.jmp 데이터 테이블에서 logNormal 열을 마우스 오른쪽 버튼으로 클릭하고 계산식을 선택합니다.
2. 분석 > 전문 모델링 > 비선형을 선택합니다.
3. logNormal을 선택하고 손실을 클릭합니다.
4. 확인을 클릭합니다.
5. "평균" 옆의 상자에 "4.72"를 입력합니다.
6. "시그마" 옆의 상자에 "0.35"를 입력합니다.
7. 시작을 클릭합니다.
8. 신뢰 한계를 클릭합니다.
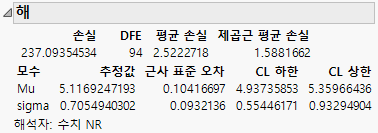
그림 15.29 해 보고서
로그 정규 모수의 최대 가능도 추정값은 평균의 경우 5.11692이고 시그마의 경우 0.7055입니다. 로그 정규 분포의 중앙값에 대한 해당 추정값은 5.11692의 역대수(e5.11692)로, 약 167입니다. 이는 기관차 엔진의 일반적인 수명을 나타냅니다.